题目内容
若一次函数y=ax+b的图象不经过第一象限，且当-2≤x≤1，y的最大值和最小值分别为1和-2，求a，b的值．
考点：一次函数的性质与图象
专题：函数的性质及应用
分析：根据题意，画出函数图象，判定函数是减函数，由最值列方程组，求出a，b的值．
解答：
解：∵一次函数y=ax+b的图象不经过第一象限，如图所示，
∴函数y=ax+b是定义域上的减函数，
又当-2≤x≤1时，y的最大值和最小值分别为1和-2，
∴
；
解得a=-1，b=-1．
解：∵一次函数y=ax+b的图象不经过第一象限，如图所示，∴函数y=ax+b是定义域上的减函数，
又当-2≤x≤1时，y的最大值和最小值分别为1和-2，
∴
|
解得a=-1，b=-1．
点评：本题考查了一次函数的图象与性质的应用问题，解题时应根据函数的图象与性质，判定出函数的增减性，从而解答问题，是容易题．
练习册系列答案
相关题目
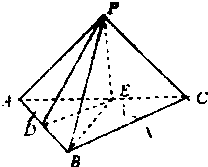如图，在三棱锥P-ABC中，AB=2，AC=BC=