题目内容
椭圆
+
=1的离心率为（ ）
| x2 |
| 25 |
| y2 |
| 9 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
考点：椭圆的简单性质
专题：圆锥曲线的定义、性质与方程
分析：首先，分清长半轴长和短半轴长，然后，求解半焦距，最后，求解离心率即可．
解答：
解：∵椭圆
+
=1，
∴a=5，b=3，
∴c=
=4，
∴c=4，
∴e=
=
，
∴椭圆的离心率为：
．
故选：D．
| x2 |
| 25 |
| y2 |
| 9 |
∴a=5，b=3，
∴c=
| a2-b2 |
∴c=4，
∴e=
| c |
| a |
| 4 |
| 5 |
∴椭圆的离心率为：
| 4 |
| 5 |
故选：D．
点评：本题重点考查了椭圆中基本量之间的关系、椭圆的简单几何性质等知识，属于基础题．
练习册系列答案
阶梯计算系列答案
相关题目
根据如图图案中的圆圈排列规则，猜想第6个图形中的圆圈个数是（ ）
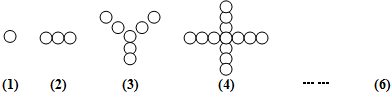
| A、20 | B、25 | C、31 | D、36 |
函数f（x）=xcos3x的导数是（ ）
| A、cos3x+3sin3x |
| B、1-3sin3x |
| C、cos3x-3xsin3x |
| D、cos3x-xsin3x |
等比数列{an}的各项均为正数，且a5．a6=9，则log3a1+log3a2+log3a3+…+log3a10（ ）
| A、12 |
| B、10 |
| C、8 |
| D、2+log35 |
设函数f（x）=x3-3ax+b（a＞0），则（ ）
A、x=
| ||
B、x=-
| ||
C、x=
| ||
D、x=-
|
已知tanα=5，则2sin2α-3sinαcosα+4cos2α的值为（ ）
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |