题目内容
13．定义在R上的函数f（x）满足：f'（x）＞2-f（x），f（0）=6，f'（x）是f（x）的导函数，则不等式exf（x）＞2ex+4（其中e为自然对数的底数）的解集为（ ）| A． | （0，+∞） | B． | （-∞，0）∪（3，+∞） | C． | （-∞，0）∪（1，+∞） | D． | （3，+∞） |
分析 令F（x）=exf（x）-2ex-4，从而求导F′（x）=ex（f（x）+f′（x）-2）＞0，从而由导数求解不等式．
解答 解：令F（x）=exf（x）-2ex-4，
则F′（x）=ex[f（x）+f′（x）-2]＞0，
故F（x）是R上的单调增函数，
而F（0）=e0f（0）-2e0-4=0，
故不等式exf（x）＞2ex+4（其中e为自然对数的底数）的解集为（0，+∞）
故选：A．
点评 本题考查函数单调性与奇偶性的结合，结合已知条件构造函数，然后用导数判断函数的单调性是解题的关键．
练习册系列答案
相关题目
3．若三棱锥的三条侧棱两两垂直，侧棱长分别为1，$\sqrt{3}$，2，且它的四个顶点在同一球面上，则此球的体积为（ ）
| A． | $\frac{{2\sqrt{2}}}{3}π$ | B． | $3\sqrt{3}π$ | C． | $\frac{{8\sqrt{2}}}{3}π$ | D． | 8π |
8．已知直线mx+ny-2=0（mn＞0）过点（1，1），则$\frac{1}{m}$+$\frac{1}{n}$有（ ）
| A． | 最小值4 | B． | 最大值4 | C． | 最小值2 | D． | 最大值2 |
如图，建立平面直角坐标系xoy，x轴在地平面上，y轴垂直于地平面，单位长度为1千米．某炮位于坐标原点．已知炮弹发射后的轨迹在方程y=kx-$\frac{1}{20}$（1+k2）x2（k＞0）表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．
5．
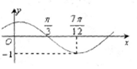函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，为了得到g（x）=sinωx的图象，则只要将f（x）的图象（ ）
函数f（x）=sin（ωx+φ）（ω＞0，|φ|＜$\frac{π}{2}$）的图象如图所示，为了得到g（x）=sinωx的图象，则只要将f（x）的图象（ ）| A． | 向左平移$\frac{π}{3}$个单位长度 | B． | 向右平移$\frac{π}{3}$个单位长度 | ||
| C． | 向右平移$\frac{π}{6}$个单位长度 | D． | 向左平移$\frac{π}{6}$个单位长度 |