题目内容
已知函数f(x)=
,则方程f(x)=2x在[0,2015]内的根的个数为 .
|
考点:根的存在性及根的个数判断
专题:计算题,函数的性质及应用
分析:由题意,当x≤1时,有3x-1=2x解得,x=1;再由当x>1时,f(x)=2x可化为f(x-1)+2=2(x-1)+2;即f(x-1)=2(x-1);即f(x-2)=2(x-2);故x=2,3,4,…,2015都是方程的根,从而得到.
解答:
解:当x≤1时,有3x-1=2x解得,x=1;
当x>1时,f(x)=2x可化为
f(x-1)+2=2(x-1)+2;即f(x-1)=2(x-1);
即f(x-2)=2(x-2);
又由x=1是方程的根知,
x=2,3,4,…,2015都是方程的根,
故有2015个根,
故答案为:2015.
当x>1时,f(x)=2x可化为
f(x-1)+2=2(x-1)+2;即f(x-1)=2(x-1);
即f(x-2)=2(x-2);
又由x=1是方程的根知,
x=2,3,4,…,2015都是方程的根,
故有2015个根,
故答案为:2015.
点评:本题考查了函数的零点与方程的根的关系应用,属于基础题.

练习册系列答案
相关题目
已知集合M={x<1},N={x|x>0},则M∩N等于( )
| A、{x|x<1} |
| B、{x|x>1} |
| C、{x|0<x<1} |
| D、∅ |
数列{an}满足a1=1,且对于任意的n∈N*都有an+1=an+a1+n,则
+
+…+
等于( )
| 1 |
| a1 |
| 1 |
| a2 |
| 1 |
| a2014 |
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示,程序框图输出的所有实数对(x,y)所对应的点都在函数( )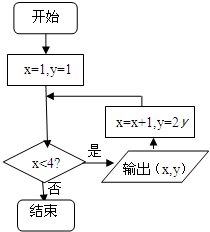

| A、y=x+1的图象上 |
| B、y=2x的图象上 |
| C、y=2x的图象上 |
| D、y=2x-1的图象上 |
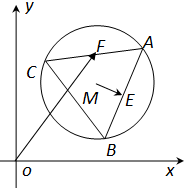 如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,
如图,已知圆M:(x-3)2+(y-3)2=4,△ABC为圆M的内接正三角形,E为边AB的中点,当正△ABC绕圆心M转动,且F是AC边上的中点,