题目内容
已知a，b，c分别为△ABC三个内角A，B，C的对边，c=
asinC+ccosA．
（1）求角A；
（2）若a=2
，△ABC的面积为
，求△ABC的周长．
| 3 |
（1）求角A；
（2）若a=2
| 3 |
| 3 |
考点：余弦定理,正弦定理
专题：三角函数的求值
分析：（1）已知等式利用正弦定理化简，根据sinC不为0，得到关系式，利用两角和与差的正弦函数公式化为一个角的三角函数值，利用特殊角的三角函数值求出A的度数即可；
（2）利用三角形面积公式列出关系式，将sinA，已知面积代入求出bc的值，再利用余弦定理列出关系式，将a，bc，cosA的值代入求出b+c的值，即可出三角形ABC周长．
（2）利用三角形面积公式列出关系式，将sinA，已知面积代入求出bc的值，再利用余弦定理列出关系式，将a，bc，cosA的值代入求出b+c的值，即可出三角形ABC周长．
解答：
解：（1）由c=
asinC+ccosA，利用正弦定理化简得：sinC=
sinAsinC+sinCcosA，
∵sinC≠0，
∴
sinA+cosA=1，即2sin（A+
）=1，
∴sin（A+
）=
，
又0＜A＜π，
∴
＜A+
＜
，
则A+
=
，即A=
；
（2）∵△ABC的面积S=
bcsinA=
，sinA=
，
∴bc=4，
由余弦定理知a2=b2+c2-2bccosA=b2+c2+bc，得a2+bc=（b+c）2，
代入a=2
，bc=4，
解得：b+c=4，
则△ABC周长为4+2
．
| 3 |
| 3 |
∵sinC≠0，
∴
| 3 |
| π |
| 6 |
∴sin（A+
| π |
| 6 |
| 1 |
| 2 |
又0＜A＜π，
∴
| π |
| 6 |
| π |
| 6 |
| 7π |
| 6 |
则A+
| π |
| 6 |
| 5π |
| 6 |
| 2π |
| 3 |
（2）∵△ABC的面积S=
| 1 |
| 2 |
| 3 |
| ||
| 2 |
∴bc=4，
由余弦定理知a2=b2+c2-2bccosA=b2+c2+bc，得a2+bc=（b+c）2，
代入a=2
| 3 |
解得：b+c=4，
则△ABC周长为4+2
| 3 |
点评：此题考查了正弦、余弦定理，三角形面积公式，熟练掌握定理及公式是解本题的关键．
练习册系列答案
阅读快车系列答案
相关题目
若集合A={0，1，2，3}，B={0，2，4}，则集合A∪B=（ ）
| A、{1，2} |
| B、{1，2，3，4} |
| C、{0，1，2，3，4} |
| D、{0} |
在棱长为3的正方体内任取一个点，则这个点到各面的距离大于1的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图所示是函数f（x）的导函数f′（x）的图象，则下列判断中正确的是（ ）
| A、函数f（x）在区间（-2，0）上是减函数 |
| B、函数f（x）在区间（1，3）上是减函数 |
| C、函数f（x）在区间（0，2）上是减函数 |
| D、函数f（x）在区间（3，4）上是增函数 |
1+C271+C272+C2727除以3所得余数为（ ）
| A、0 | B、1 | C、2 | D、3 |
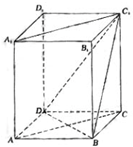如图，四棱柱ABCD-A1B1C1D1的底面是正方形，且侧棱和底面垂直．