题目内容
已知函数f(x)=x2+
.
(1)求证:f(x)在x∈[1,+∞)上是增函数;
(2)当x>0时,若f(x)≥f(m)恒成立,求正实数m的值.
| 2 |
| x |
(1)求证:f(x)在x∈[1,+∞)上是增函数;
(2)当x>0时,若f(x)≥f(m)恒成立,求正实数m的值.
考点:函数恒成立问题
专题:函数的性质及应用
分析:(1)求函数的导数,利用函数单调性和导数之间的关系即可证明f(x)在x∈[1,+∞)上是增函数;
(2)当x>0时,若f(x)≥f(m)恒成立,则f(m)为函数的最小值,然后建立方程关系即可求正实数m的值.
(2)当x>0时,若f(x)≥f(m)恒成立,则f(m)为函数的最小值,然后建立方程关系即可求正实数m的值.
解答:
解:(1)∵f(x)=x2+
.
∴f'(x)=2x-
=
,
当x∈[1,+∞)时,f'(x)≥0,
即函数f(x)在x∈[1,+∞)上是增函数;
(2)当x>0时,若f(x)≥f(m)恒成立,
则f(x)min≥f(m)恒成立,
由(1)知当0<x<1时,f'(x)<0,即此时函数单调递减,
∴当x=1时,函数f(x)取得极小值,同时也是在(0,+∞)上的最小值,
即f(1)=1+2=3,
∴若f(x)≥f(m)恒成立,
则f(m)为函数的最小值,
即正实数m=1.
| 2 |
| x |
∴f'(x)=2x-
| 2 |
| x2 |
| 2x3-2 |
| x2 |
当x∈[1,+∞)时,f'(x)≥0,
即函数f(x)在x∈[1,+∞)上是增函数;
(2)当x>0时,若f(x)≥f(m)恒成立,
则f(x)min≥f(m)恒成立,
由(1)知当0<x<1时,f'(x)<0,即此时函数单调递减,
∴当x=1时,函数f(x)取得极小值,同时也是在(0,+∞)上的最小值,
即f(1)=1+2=3,
∴若f(x)≥f(m)恒成立,
则f(m)为函数的最小值,
即正实数m=1.
点评:本题主要考查函数单调性的判断和应用,利用不等式恒成立转化为求函数的最值是解决本题的关键.

练习册系列答案
相关题目
 根据如图所示的三视图画出对应的几何体.
根据如图所示的三视图画出对应的几何体.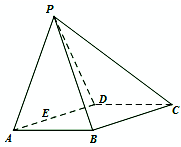 如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点.
如图所示,在四棱锥P-ABCD中,四边形ABCD为菱形,△PAD为等边三角形,平面PAD⊥平面ABCD,且∠DAB=60°,AB=2,E为AD的中点. 如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
如图,在四棱锥P-ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.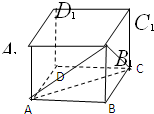 已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高.
已知正方体ABCD-A1B1C1D1的棱长是a,求三棱锥B-AB1C的高. 在△ABC中,∠BAC=120°,AB=
在△ABC中,∠BAC=120°,AB=