题目内容

下列命题：①有一个实数不能做除数； ②棱柱是多面体； ③所有方程都有实数解；  ④有些三角形是锐角三角形；其中特称命题的个数为（　　）
A、1B、2C、3D、4
考点：命题的真假判断与应用
专题：简易逻辑
分析：利用特称命题与全称命题的定义即可判断出．
解答： 解：①有一个实数不能做除数，是特称命题；
②棱柱是多面体，属于全称命题；
 ③所有方程都有实数解，属于全称命题；
  ④有些三角形是锐角三角形，属于特称命题．
综上可知：只有①④属于特称命题．
故选：B．
点评：本题考查了特称命题与全称命题的意义，属于基础题．
练习册系列答案
相关题目
函数f（x）=（m-1）lnx+mx2+1（m∈R）
（1）讨论f（x）的单调性；
（2）若对任意的x1＞x2＞0，总有f（x1）-f（x2）＞2（x1-x2）恒成立，求实数m的取值范围．
已知⊙M经过双曲线S：
x2
9
-
y2
16
=1的一个顶点和一个焦点，圆心M在双曲线上S上，则圆心M到双曲线S的中心的距离为（　　）
A、
13
4
或
7
3
B、
15
4
或
8
3
C、
13
3
D、
16
3
已知m，n是不重合的直线，α，β是不重合的平面，给出下列命题：
①若m⊥α，m?β，则α⊥β；
②若m?α，n?α，m∥β，n∥β，则α∥β；
③如果m?α，n?α，m，n是异面直线，则n与α相交；
④若α∩β=m，n∥m，且n?β，则n∥α，且n∥β．
其中正确命题的个数是（　　）
A、1B、2C、3D、4
在5×5的棋盘中，放入3颗黑子和2颗白子，它们均不在同一行且不在同一列，则不同的排列方法种数为（　　）
A、150B、200
C、600D、1200
已知函数f（x）=
ax3-3
2x2+1
（a＞2），若在区间[1，2]上f（x）＞0恒成立，求a的取值范围．
对于一切x∈[-2，
1
2
]，不等式ax3-x2+x+1≥0恒成立，求实数a的取值范围．
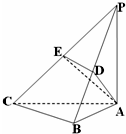已知三棱锥P-ABC，∠PAC=∠ABC=90°，PA=AC=2BC，平面PAC⊥平面ABC，D、E分别是PB、PC的中点．
（Ⅰ）求证：BC⊥平面PAB；
（Ⅱ）求二面角P-ED-A的余弦值．
已知函数f（x）=x2+
2
x
．
（1）求证：f（x）在x∈[1，+∞）上是增函数； 
（2）当x＞0时，若f（x）≥f（m）恒成立，求正实数m的值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网