题目内容
15.从某病毒爆发的疫区返回本市若干人,为了迅速甄别是否有人感染病毒,对这些人抽血,并将血样分成4组,每组血样混合在一起进行化验.(Ⅰ)若这些人中有1人感染了病毒.
①求恰好化验2次时,能够查出含有病毒血样组的概率;
②设确定出含有病毒血样组的化验次数为X,求E(X).
(Ⅱ)如果这些人中有2人携带病毒,设确定出全部含有病毒血样组的次数Y的均值E(Y),请指出(Ⅰ)②中E(X)与E(Y)的大小关系.(只写结论,不需说明理由)
分析 (Ⅰ)①由已知能求出恰好化验2次时,就能够查出含有病毒血样的组的概率.
②确定出含有病毒血样组的次数为X,则X的可能取值为1,2,3,分别求出相应的概率,由此能求出X的分布列和E(X).
(Ⅱ)由题意得E(X)<E(Y).
解答 解:(Ⅰ)①恰好化验2次时,就能够查出含有病毒血样的组为事件A,
由题意得P(A)=$\frac{3}{4}×\frac{1}{3}$=$\frac{1}{4}$.
恰好化验2次时,就能够查出含有病毒血样的组的概率为$\frac{1}{4}$.(4分)
②确定出含有病毒血样组的次数为X,则X的可能取值为1,2,3,
P(X=1)=$\frac{1}{4}$,
P(X=2)=$\frac{3}{4}×\frac{1}{3}$=$\frac{1}{4}$,
P(X=3)=$\frac{3}{4}×\frac{2}{3}×\frac{1}{2}$+$\frac{3}{4}×\frac{2}{3}×(1-\frac{1}{2})$=$\frac{1}{2}$.
则X的分布列为:
| X | 1 | 2 | 3 |
| P | $\frac{1}{4}$ | $\frac{1}{4}$ | $\frac{1}{2}$ |
(Ⅱ)E(X)<E(Y).(13分)
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,是中档题,解题时要认真审题,在历年高考中都是必考题型之一.

练习册系列答案
 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
6.已知点P(x,y)在不等式组$\left\{\begin{array}{l}{x-2≤0}\\{y-1≤0}\\{x+2y-2≥0}\end{array}\right.$,表示的平面区域上运动,则$z=\frac{2x+y-12}{x-4}$取值范围是( )
| A. | [-2,-1] | B. | [-2,1] | C. | [-1,2] | D. | $[\frac{11}{4},4]$ |
3.已知集合A、B是非空集合且A⊆B,则下列说法错误的是( )
| A. | ?x0∈A,x0∈B | B. | ?x0∈A,x0∈B | C. | A∩B=A | D. | A∩(∁uB)≠∅ |
5.已知复数$z=\frac{i}{i+1}$,那么复数z对应的点位于复平面内的( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
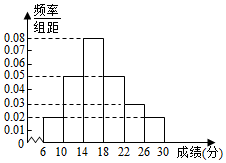 某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.
某省去年高三200000名考生英语听力考试服从正态分布N(17,9),现从某校高三年级随机抽取50名考生的成绩,发现全部介于[6,30]之间,将成绩按如图方式分成6组:第1组[6,10),第2组[10,14),…,第6组[26,30),如图是按上述分组方法得到的频率分布直方图.