题目内容
顶点在原点，始边与x轴正方向重合的角α=-
的终边在（ ）
| 19π |
| 6 |
| A、第一象限 | B、第二象限 |
| C、第三象限 | D、第四象限 |
考点：象限角、轴线角
专题：计算题
分析：由题意可得：-
=-4π+
，结合象限角的定义可得结论．
| 19π |
| 6 |
| 5π |
| 6 |
解答：
解：由题意可得：-
=-4π+
，
∵
＜
＜π
故角-
是第二象限角，
故选B．
| 19π |
| 6 |
| 5π |
| 6 |
∵
| π |
| 2 |
| 5π |
| 6 |
故角-
| 19π |
| 6 |
故选B．
点评：本题考查象限角的概念．
练习册系列答案
相关题目
已知椭圆的两个焦点和短轴的两个端点恰好为一个正方形的四个顶点，则该椭圆的离心率为（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
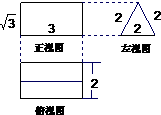已知某个几何体的三视图如图所示，试根据图中所标出的尺寸（单位：cm），可得这个几何体的表面积是（ ）A、18+
| ||
B、18+2
| ||
C、24+2
| ||
D、24+2
|
已知曲线C1：x2+y2-2x=0和曲线C2：y=xcoxθ-1（θ为锐角），则C1与C2的位置关系为（ ）
| A、相切 | B、相交 |
| C、相离 | D、以上情况均有可能 |
某几何体的三视图如图所示，其中俯视图是个半圆，则该几何体的体积为（ ）A、
| ||||
| B、π | ||||
C、
| ||||
D、
|
在△ABC中，角A，B，C所对边长分别为a，b，c，若a2+b2=2c2，则角C的最大值为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
直线x+
y-2=0被圆（x-1）2+y2=1所截得的弦长为（ ）
| 3 |
| A、1 | ||
B、
| ||
C、
| ||
| D、2 |