题目内容
3.为了解某校学生的视力情况,现采用随机抽样的方式从该校的A,B两班中各抽5名学生进行视力检测,检测的数据如下:A班5名学生的视力检测结果:4.3,5.1,4.6,4.1,4.9.
B班5名学生的视力检测结果:5.1,4.9,4.0,4.0,4.5.
(1)分别计算两组数据的平均数,从计算结果看,哪个班的学生视力较好?并计算A班5名学生视力的方差;
(2)现从B班的上述5名学生中随机选取2名,求这2名学生中至少有1名学生的视力低于4.5的概率.
分析 (1)分别求出A班5名学生视力平均数和B班5名学生视力平均数,从计算结果看,A个班的学生视力较好,再求出A班5名学生视力的方差.
(2)从B班的上述5名学生中随机选取2名,基本事件总数n=${C}_{5}^{2}$=10,这2名学生中至少有1名学生的视力低于4.5对立事件是这2名学生的视力都不低于4.5,用列举法求出这2名学生的视力都不低于4.5,包含的基本事件个数,由此能求出这2名学生的视力都不低于4.5的概率.
解答 解:(1)A班5名学生视力平均数$\overline{{x}_{A}}$=$\frac{4.3+5.1+4.6+4.1+4.9}{5}$=4.6,
B班5名学生视力平均数$\overline{{x}_{B}}$=$\frac{5.1+4.9+4.0+4.0+4.5}{5}$=4.5,
从计算结果看,A个班的学生视力较好,
A班5名学生视力的方差:
${{S}_{A}}^{2}$=$\frac{1}{5}$[(4.3-4.6)2+(5.1-4.6)2+(4.6-4.6)2+(4.1-4.6)2+(4.9-4.6)2]=0.136.
(2)从B班的上述5名学生中随机选取2名,基本事件总数n=${C}_{5}^{2}$=10,
这2名学生中至少有1名学生的视力低于4.5对立事件是这2名学生的视力都不低于4.5,
这2名学生的视力都不低于4.5,包含的基本事件有(5.1,4.5),(5.1,4.9),(4.9,4.5),
∴这2名学生的视力都不低于4.5的概率:
p=1-$\frac{3}{10}$=$\frac{7}{10}$.
点评 本题考查概率的求法,是基础题,解题时要认真审题,注意列举法的合理运用.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.在复平面内,复数$\frac{2}{1-i}$-2对应的点位于( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
8.若(x2-$\frac{1}{{x}^{3}}$)n的展开式中存在常数项,则n可以为( )
| A. | 8 | B. | 9 | C. | 10 | D. | 11 |
13.在正四棱锥P-ABCD中,PA=2,E为PC的中点,若异面直线PA与BE所成角为45°,则四棱锥P-ABCD的高为( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | $\frac{2\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | 2$\sqrt{3}$ |
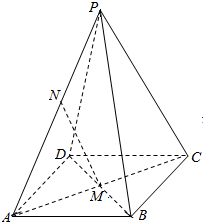 (理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.
(理科做)如图,正四棱锥P-ABCD中,PA=BD,点M为AC,BD的交点,点N为AP中点.