题目内容
8.已知向量$\overrightarrow{m}$=(2cos2x,$\sqrt{3}$),$\overrightarrow{n}$=(1,sin2x),函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$.(Ⅰ)求函数f(x)的最小正周期和单调递减区间;
(Ⅱ)在△ABC中,a,b,c分别是角A,B,C的对边,且f(C)=3,c=1,△ABC的面积为$\frac{\sqrt{3}}{2}$,且a>b,求a,b的值.
分析 (Ⅰ)根据向量数量积的坐标公式结合三角函数的辅助角公式将函数进行化简,结合函数周期和单调性的性质进行求解即可.
(Ⅱ)根据条件f(C)=3,求出C的大小,结合余弦定理以及三角形的面积公式进行化简求解即可.
解答 解:(Ⅰ)f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$=(2cos2x,$\sqrt{3}$)•(1,sin2x)=2cos2x+$\sqrt{3}$sin2x
=cos2x+1+$\sqrt{3}$sin2x=2sin(2x+$\frac{π}{6}$)+1,
∴函数f(x)的最小周期T=$\frac{2π}{2}$=π.
由2kπ+$\frac{π}{2}$≤2x+$\frac{π}{6}$≤2kπ+$\frac{3π}{2}$,k∈Z,
得kπ+$\frac{π}{6}$≤x≤kπ+$\frac{2π}{3}$,k∈Z,
则f(x)的单调递减区间[kπ+$\frac{π}{6}$,kπ+$\frac{2π}{3}$],k∈Z.
(Ⅱ)∵f(C)=3,
∴f(C)=2sin(2C+$\frac{π}{6}$)+1=3,
∴sin(2C+$\frac{π}{6}$)=1,
∴C是三角形内角,
∴2C+$\frac{π}{6}$=$\frac{π}{2}$,即C=$\frac{π}{6}$,
∴cosC=$\frac{{b}^{2}+{a}^{2}-{c}^{2}}{2ab}$=$\frac{\sqrt{3}}{2}$,
即:a2+b2-$\sqrt{3}ab=1$(1).
由${S_{△ABC}}=\frac{1}{2}absin\frac{π}{6}=\frac{1}{4}ab=\frac{{\sqrt{3}}}{2}⇒ab=2\sqrt{3}$,代入(1)得a2+b2=7,
联立方程组消去b可得:a2+$\frac{12}{{a}^{2}}$=7,解之得a2=3或4,
则a=$\sqrt{3}$或2,
∵a>b,∴a=2,b=$\sqrt{3}$.
点评 本题主要考查向量数量积与三角函数的综合问题,利用辅助角公式以及余弦定理将函数进行化简是解决本题的关键.

 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案| A. | [-2,1] | B. | (-2,1] | C. | [-3,3) | D. | (-2,3) |
| A. | a<b<0 | B. | a<c<b | C. | b<c<a | D. | b<a<c |
| A. | 2 | B. | 4 | C. | $\frac{15}{2}$ | D. | $\frac{17}{2}$ |
| A. | $\frac{3}{4}$ | B. | $-\frac{1}{3}$ | C. | $-\frac{3}{4}$ | D. | 4 |
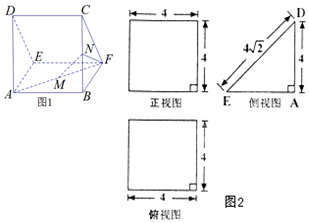 一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,
一个多面体的直观图(图1)及三视图(图2)如图所示,其中M、N分别是AF、BC的中点,