Question

19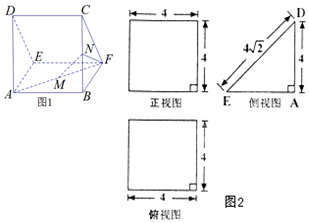．一个多面体的直观图（图1）及三视图（图2）如图所示，其中M、N分别是AF、BC的中点，
（1）求证：MN∥平面CDEF；
（2）求点B到平面MNF的距离．

Answer 1

分析 由三视图可知：平面ABCD⊥平面ABFE，AD⊥平面ABFE，四边形ABCD是边长为4的正方形，底面ABFE是边长为2的正方形，M，N分别为AF，BC的中点．
（1）取BF的中点P，连接MP，NP．又M，N分别为AF，BC的中点．利用三角形中位线定理、面面平行的判定定理可得：平面MNP∥平面CDEF，即可证明MN∥平面CDEF．
（2）利用等体积法，求点B到平面MNF的距离．

解答 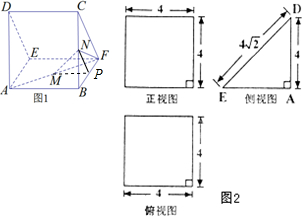（1）证明：由三视图可知：平面ABCD⊥平面ABFE，AD⊥平面ABFE．
四边形ABCD是边长为2的正方形，底面ABFE是边长为4的正方形，M，N分别为AF，BC的中点．
取BF的中点P，连接MP，NP．
又M，N分别为AF，BC的中点．
∴NP∥CF，MP∥AB，
又AB∥EF，
可得MP∥EF．
又MP∩NP=P，MP?平面CDEF，NP?平面CDEF．
∴平面MNP∥平面CDEF；
∴MN∥平面CDEF．
（2）解：△MNF中，NM⊥MF，MF=2$\sqrt{2}$，MN=$\sqrt{16+4-8}$=2$\sqrt{3}$，S_△MNF=$\frac{1}{2}×2\sqrt{2}×2\sqrt{3}$=2$\sqrt{6}$，
设点B到平面MNF的距离为h，则$\frac{1}{3}×2\sqrt{6}h$=$\frac{1}{3}×\frac{1}{2}×2\sqrt{2}×2\sqrt{2}×2$，∴h=$\frac{4\sqrt{6}}{3}$．

点评 本题考查线面平行的判定，考查点到平面距离的计算，考查等体积方法的运用，属于中档题．