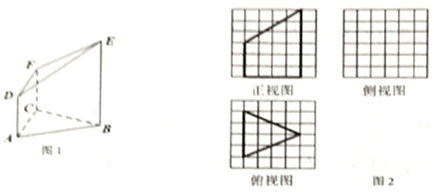
题目内容
16.以下四个命题中,错误命题的序号是( )| A. | △ABC中,若a>b,则sinA>sinB | |
| B. | 函数y=f(x)在x=x0处取得极值的充要条件是f'(x0)=0 | |
| C. | 等差数列{an}中,a4=4,a5+a11=16则a12=12 | |
| D. | 双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点到渐近线的距离3. |
分析 根据正弦定理,可判断A;根据函数极值点的性质,可判断B;根据等差数列的性质,可判断C;根据双曲线的性质,可判断D.
解答 解:△ABC中,若a>b?2RsinA>2RsinB?sinA>sinB,故A正确;
f'(x0)=0是函数y=f(x)在x=x0处取得极值的必要不充分条件,故B错误;
等差数列{an}中,a4=4,a5+a11=16,则a12=a5+a11-a4=12,故C正确;
双曲线$\frac{x^2}{16}-\frac{y^2}{9}=1$的焦点到渐近线的距离为b=3,故D正确;
故选:B
点评 本题以命题的真假判断与应用为载体,考查了正弦定理,函数的极值,等差数形的性质,双曲线的性质等知识点,难度中档.

练习册系列答案
 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
7.已知点A(x0,y0)是抛物线y2=2px(p>0)上一点,且它在第一象限内,焦点为F,O坐标原点,若|AF|=$\frac{3p}{2}$,|AO|=2$\sqrt{3}$,则此抛物线的准线方程为( )
| A. | x=-4 | B. | x=-3 | C. | x=-2 | D. | x=-1 |
4.设a,b∈R,函数f(x)=ax+b(0≤x≤1),则f(x)>0恒成立是a+2b>0成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 即不充分也不必要条件 |
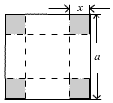 如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.
如图所示,把一块边长是a的正方形铁片的各角切去大小相同的小正方形,再把它的边沿着虚线折转作成一个无盖方底的盒子,当盒子的容积最大时,切去的正方形的边长x为$\frac{a}{6}$.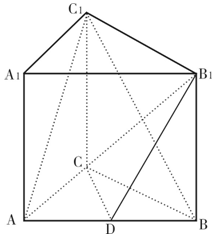 如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.
如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=3,BC=4,AB=5,点D是AB的中点.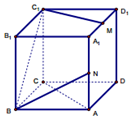 如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )
如图,已知正方体ABCD-A1B1C1D1,M,N分别为A1D1和AA1的中点,则下列四种说法中正确的个数为( )