题目内容
13．过曲线y=$\sqrt{x}$上的点（4，2）的切线方程是（ ）| A． | x+4y+4=0 | B． | x-4y-4=0 | C． | x-4y+4=0 | D． | x+4y-4=0 |
分析 求出导数，求得切线的斜率，由点斜式方程可得所求切线的方程．
解答 解：y=$\sqrt{x}$的导数为y′=$\frac{1}{2\sqrt{x}}$，
可得过点（4，2）的切线斜率为k=$\frac{1}{4}$，
则所求切线的方程为y-2=$\frac{1}{4}$（x-4），
即为x-4y+4=0，
故选：C．
点评 本题考查导数的运用：求切线的方程，考查导数的几何意义：函数在某点处的导数即为曲线在该点处切线的斜率，正确求导和运用直线方程是解题的关键，属于基础题．
练习册系列答案
相关题目
5．直线y=kx-2交抛物线y2=8x于A、B两点，若AB中点横坐标为2，则|AB|为（ ）
| A． | $\sqrt{15}$ | B． | $2\sqrt{15}$ | C． | $\sqrt{42}$ | D． | $3\sqrt{15}$ |
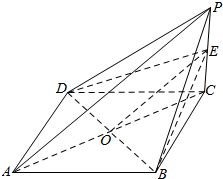如图所示，在四棱锥P-ABCD中，四边形ABCD是边长为2的正方形，平面ABCD⊥平面PCD，∠PCD=90°，PC=1.5，E是侧棱PC上的动点．
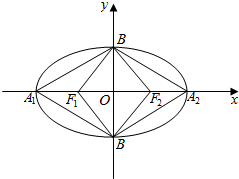如图所示，椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0），A1、A2、B1、B2、F1、F2分别是其左右顶点，上下顶点和左右焦点，四边形A1B1A2B2的面积是四边形B1F2B2F1面积的2倍．