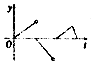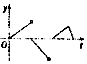题目内容
19.函数f(x)=lg(2sinx+1)+$\sqrt{2cosx-1}$的定义域是(2kπ-$\frac{π}{6}$,2kπ+$\frac{π}{3}$],k∈Z.分析 根据函数f(x)列出使解析式有意义的不等式组$\left\{\begin{array}{l}{2sinx+1>0}\\{2cosx-1≥0}\end{array}\right.$,求出解集即可.
解答 解:函数f(x)=lg(2sinx+1)+$\sqrt{2cosx-1}$,
∴$\left\{\begin{array}{l}{2sinx+1>0}\\{2cosx-1≥0}\end{array}\right.$,
即$\left\{\begin{array}{l}{sinx>-\frac{1}{2}}\\{cosx≥\frac{1}{2}}\end{array}\right.$,
解得2kπ-$\frac{π}{6}$<x≤2kπ+$\frac{π}{3}$,k∈Z;
∴函数f(x)的定义域是(2kπ-$\frac{π}{6}$,2kπ+$\frac{π}{3}$],k∈Z.
故答案为:(2kπ-$\frac{π}{6}$,2kπ+$\frac{π}{3}$],k∈Z.
点评 本题考查了根据函数的解析式求定义域的应用问题,是基础题.

练习册系列答案
 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案
相关题目
10.设函数f(x)的定义域为R,且|f(x)|是偶函数,则下列结论中正确的是( )
| A. | f(x)是偶函数 | B. | f(x)是奇函数 | ||
| C. | |f(x-1)|的图象关于直线x=1对称 | D. | |f(x)+1|的图象关于点(0,1)对称 |
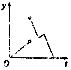
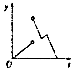
 如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )
如图,一个正五角星薄片(其对称轴与水面垂直)匀速地升出水面,记t时时刻五角星露出水面部分的图形面积为S(t)(S(0)=0),则导函数y=S′(t)的图象大致为( )