题目内容
8.如图所示,在边长为1的正方形f(x)中任取一点f(x),则点[-1,1)恰好取自阴影部分的概率为$\frac{1}{6}$.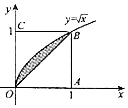
分析 求出正方形OABC的面积,阴影部分由函数y=x与y=$\sqrt{x}$围成,由定积分公式计算阴影部分的面积,由几何概型公式计算即可.
解答 解:根据题意,该题是几何概型的应用问题,
正方形OABC的面积为1×1=1,
而阴影部分由函数y=x与y=$\sqrt{x}$围成,其面积为
${∫}_{0}^{1}$($\sqrt{x}$-x)dx=($\frac{2}{3}$${x}^{\frac{3}{2}}$-$\frac{1}{2}$x2)${|}_{0}^{1}$=$\frac{1}{6}$;
则所求的概率为P=$\frac{1}{6}$.
故答案为:$\frac{1}{6}$.
点评 本题考查了几何概型的计算问题,涉及定积分在求面积中的应用,是基础题.

练习册系列答案
相关题目
16.函数y=x2+bx-4在(-∞,-1]上是减函数,在[-1,+∞)上是增函数,则( )
| A. | b<0 | B. | b>0 | C. | b=0 | D. | b的符号不定 |
17.函数$f(x)=3sin({\frac{2π}{3}-2x})$的一个单调递增区间是( )
| A. | $[{\frac{7π}{12},\frac{13π}{12}}]$ | B. | $[{\frac{π}{12},\frac{7π}{12}}]$ | C. | $[{-\frac{π}{2},\frac{π}{2}}]$ | D. | $[{-\frac{5π}{6},\frac{π}{6}}]$ |
17.在某化学反应的中间阶段,压力保持不变,温度从1℃变化到5℃,反应结果如表所示(x表示温度,y代表结果):
(1)求化学反应的结果y对温度x的线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$;
(2)判断变量x与y之间是正相关还是负相关,并预测当温度到达10℃时反应结果为多少?
附:线性回归方程中$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
| x | 1 | 2 | 3 | 4 | 5 |
| y | 3 | 5 | 7 | 10 | 11 |
(2)判断变量x与y之间是正相关还是负相关,并预测当温度到达10℃时反应结果为多少?
附:线性回归方程中$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$,$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$,$\stackrel{∧}{a}$=$\overline{y}$-b$\overline{x}$.
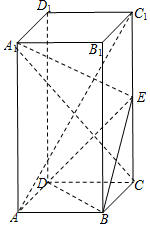 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.