题目内容
11.已知双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1的左焦点为F,点P为双曲线右支上一点,点A满足$\overrightarrow{AP}$•$\overrightarrow{AF}$=0,则点A到原点的最近距离为( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |
分析 设F'为双曲线的右焦点,M为PF的中点,则|PF|-|PF'|=2$\sqrt{2}$,|OM|=$\frac{1}{2}$|PF'|,点A在以PF为直径的圆上,故当O,A,M共线时,可得OA取得最小值MA-OM.
解答 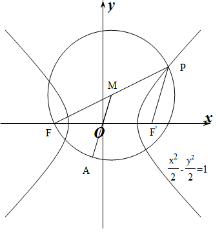 解:双曲线的左焦点为F(-2,0),右焦点为F′(2,0),
解:双曲线的左焦点为F(-2,0),右焦点为F′(2,0),
连接PF′,PF,设PF的中点为M,
∵$\overrightarrow{AP}$•$\overrightarrow{AF}$=0,
∴点A在以PF为直径的圆M上,
∴当AOM三点共线时,OA取得最小值,最小值为MA-OM.
设圆M的半径为r,则PF=2r,MA=r.
∵P在双曲线$\frac{{x}^{2}}{2}$-$\frac{{y}^{2}}{2}$=1上,
∴PF-PF′=2$\sqrt{2}$,
∴PF′=2r-2$\sqrt{2}$,
∵OM是△PFF′的中位线,
∴OM=$\frac{1}{2}$PF′=r-$\sqrt{2}$,
∴MA-OM=r-(r-$\sqrt{2}$)=$\sqrt{2}$.
故选:B.
点评 本题考查两点的距离的最小值的求法,注意运用双曲线的定义和圆的性质,及三点共线取得最小值,考查运算能力,属于中档题

练习册系列答案
相关题目
2.下列选项中方程表示图中曲线的是( )
| A. |  x2+y2=1 | B. |  x2-y2=0 | C. |  y=|x| | D. |  lgx+lgy=0 |
16.函数y=x2+bx-4在(-∞,-1]上是减函数,在[-1,+∞)上是增函数,则( )
| A. | b<0 | B. | b>0 | C. | b=0 | D. | b的符号不定 |
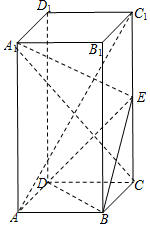 在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.
在正四棱柱ABCD-A1B1C1D1中,AA1=2AB,E为棱CC1上的动点.