Question

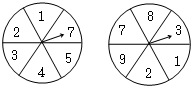如右图所示，在两个圆盘中，指针在本圆盘每个数所在区域的机会均为

1

6

，那么两个指针至少有一落在奇数所在区域的概率是（　　）

• A、

  8

  9

• B、

  2

  9

• C、

  4

  9

• D、

  1

  3

Answer 1

考点：几何概型

专题：概率与统计

分析：由题意知本题是一个相互独立事件同时发生的概率，指针在本圆盘每个数所在区域的机会均等，可以用几何概型公式求出概率，
对于第一个圆盘和第二个圆盘来说指针落在偶数区域的概率一样，根据相互独立事件同时发生的概率得到结果．

解答： 解：根据题意，可得指针在本圆盘每个数所在区域的机会均等，
∴对于第一个圆盘来说指针落在偶数区域的概率是

2

6

=

1

3

，
对于第二个圆盘来说指针落在偶数区域的概率是

2

6

=

1

3

，
∴两个指针同时落在偶数所在区域的概率是

1

3

×

1

3

=

1

9

，
∴两个指针至少有一落在奇数所在区域的概率是1-

1

9

=

8

9

；
故选A．

点评：本题是一个相互独立事件同时发生的概率和几何概型，对于至多、至少问题的概率求法．通常通过求对立事件的概率来求其概率．