题目内容
已知集合A={a,b,c},B{x|1≤x≤9且x∈N}若映射f:A→B满足f(a)≤f(b)≤f(c)且f(a)+f(b)+f(c)=12,则这样的映射个数为( )
| A、12 | B、11 | C、10 | D、9 |
考点:映射
专题:函数的性质及应用
分析:根据已知中,集合A={a,b,c},B{x|1≤x≤9且x∈N}若映射f:A→B满足f(a)≤f(b)≤f(c)且f(a)+f(b)+f(c)=12,列举出所有满足条件的映射,可得答案.
解答:
解:∵集合A={a,b,c},B{x|1≤x≤9且x∈N},
映射f:A→B满足f(a)≤f(b)≤f(c)且f(a)+f(b)+f(c)=12,
∴f(a)=1,f(b)=2,f(c)=9,
f(a)=1,f(b)=3,f(c)=8,
f(a)=1,f(b)=4,f(c)=7,
f(a)=1,f(b)=5,f(c)=6,
f(a)=2,f(b)=2,f(c)=8,
f(a)=2,f(b)=3,f(c)=7,
f(a)=2,f(b)=4,f(c)=6,
f(a)=2,f(b)=5,f(c)=5,
f(a)=3,f(b)=3,f(c)=6,
f(a)=3,f(b)=4,f(c)=5,
f(a)=4,f(b)=4,f(c)=4,
共11个,
故选:B
映射f:A→B满足f(a)≤f(b)≤f(c)且f(a)+f(b)+f(c)=12,
∴f(a)=1,f(b)=2,f(c)=9,
f(a)=1,f(b)=3,f(c)=8,
f(a)=1,f(b)=4,f(c)=7,
f(a)=1,f(b)=5,f(c)=6,
f(a)=2,f(b)=2,f(c)=8,
f(a)=2,f(b)=3,f(c)=7,
f(a)=2,f(b)=4,f(c)=6,
f(a)=2,f(b)=5,f(c)=5,
f(a)=3,f(b)=3,f(c)=6,
f(a)=3,f(b)=4,f(c)=5,
f(a)=4,f(b)=4,f(c)=4,
共11个,
故选:B
点评:本题考查的知识点是映射,正确理解映射的定义,不重不漏的列举出所有满足条件的映射,是解答的关键.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
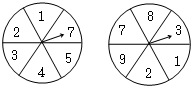 如右图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均为
如右图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均为| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|