题目内容
设全集U=R,集合A={x||2x-1|+|x-2|<3},B={y|y=x3-x2,x∈A},求(∁UA)∩B.
考点:交、并、补集的混合运算
专题:集合
分析:通过讨论x的范围,解不等式从而求出集合A,通过求导得到y=x3-x2的单调性,从而求出集合B,进而求出(∁UA)∩B.
解答:
解:当x<
时,原不等式变形为1-2x+2-x<3,解得x>0,
∴0<x<
,
当
≤x≤2时,原不等式变形为2x-1+2-x<3,解得x<2,
∴
≤x<2,
当x≥2时,原不等式变形为2x-1+x-2<3,解得x<2,
∴x∈∅,
综上,A={x|0<x<2},
由y′=(x3-x2)′=3x2-2x=0,
解得:x=0或x=
,
当x∈(0,
)时,y′<0;x∈(
,2)时,y′>0,
∴y=x3-x2,x∈A={x|0<x<2}在(0,
)单减,在(
,2)单增.
∴y∈[-
,4),即B={y|-
≤y<4},
∴(∁UA)∩B={x|-
≤x≤0或2≤x<4}.
| 1 |
| 2 |
∴0<x<
| 1 |
| 2 |
当
| 1 |
| 2 |
∴
| 1 |
| 2 |
当x≥2时,原不等式变形为2x-1+x-2<3,解得x<2,
∴x∈∅,
综上,A={x|0<x<2},
由y′=(x3-x2)′=3x2-2x=0,
解得:x=0或x=
| 2 |
| 3 |
当x∈(0,
| 2 |
| 3 |
| 2 |
| 3 |
∴y=x3-x2,x∈A={x|0<x<2}在(0,
| 2 |
| 3 |
| 2 |
| 3 |
∴y∈[-
| 4 |
| 27 |
| 4 |
| 27 |
∴(∁UA)∩B={x|-
| 4 |
| 27 |
点评:本题考查了集合的运算,考查了分类讨论思想,函数的单调性,是一道中档题.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
设四面体ABCD的六条棱的长分别为1,1,
,
,
和
,则其外接球的表面积为( )
| 2 |
| 2 |
| 2 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
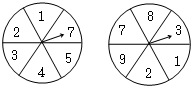 如右图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均为
如右图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均为| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|