题目内容
在△ABC中,向量
=(sinC,-1),
=(cosA+cosB,sinA+sinB),若
⊥
,判别△ABC形状.
| m |
| n |
| m |
| n |
考点:三角形的形状判断
专题:解三角形,平面向量及应用
分析:由
•
=0以及sinB=sin(A+C)求得sinA=sinCcosB-cosCsinA.再根据 sinA=sin(B+C),求得cosC(sinA+sinB)=0,可得 C=90°,△ABC为直角三角形.
| m |
| n |
解答:
解:由
⊥
,可得
•
=sinC(cosA+cosB)+(-1)(sinA+sinB)=0,
即 sinC(cosA+cosB)=sinA+sinB=sinA+sin(A+C)=sinA+sinAcosC+cosAsinC,
∴sinA=sinCcosB-cosCsinA,即 sin(B+C)=sinCcosB-cosCsinA,
即 sinBcosC+cosBsinC=sinCcosB-cosCsinA,∴cosC(sinA+sinB)=0.
由于sinA+sinB>0,∴cosC=0,∴C=90°,∴△ABC为直角三角形.
| m |
| n |
| m |
| n |
即 sinC(cosA+cosB)=sinA+sinB=sinA+sin(A+C)=sinA+sinAcosC+cosAsinC,
∴sinA=sinCcosB-cosCsinA,即 sin(B+C)=sinCcosB-cosCsinA,
即 sinBcosC+cosBsinC=sinCcosB-cosCsinA,∴cosC(sinA+sinB)=0.
由于sinA+sinB>0,∴cosC=0,∴C=90°,∴△ABC为直角三角形.
点评:本题考查三角形的形状判断,着重考查两角和的正弦,求得cosC(sinB+sinA)=0是转化的关键,属于中档题.

练习册系列答案
 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
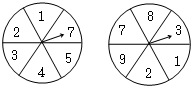 如右图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均为
如右图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均为| 1 |
| 6 |
A、
| ||
B、
| ||
C、
| ||
D、
|
函数f(x)=ln(3x-2)的定义域是( )
| A、[1,+∞) | ||
B、(
| ||
C、[
| ||
D、(
|