题目内容
已知函数f(x)=2lnx-x2+2x
(Ⅰ)求函数f(x)的图象在x=1处的切线的方程;
(Ⅱ)若函数g(x)=
x3+x2[f′(x)+2x-
+m]在区间(1,3)上不是单调函数,求m的取值范围;
(Ⅲ)若在区间(1,+∞)上,函数h(x)=
f(x)+ax2-x的图象恒在直线y=2ax(x∈R)的下方,求实数a的取值范围.
(Ⅰ)求函数f(x)的图象在x=1处的切线的方程;
(Ⅱ)若函数g(x)=
| 1 |
| 3 |
| 4 |
| x |
(Ⅲ)若在区间(1,+∞)上,函数h(x)=
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)只须求出其斜率的值即可,故先利用导数求出在x=1处的导函数值,再结合导数的几何意义即可求出切线的斜率.从而问题解决
(Ⅱ)求出g′(x),因为g(x)在区间(1,3)上不单调,所以g′(x)改变符号,从而得到m所满足的条件.
(Ⅲ)将图象的位置关系转化为不等式恒成立;通过构造函数,对新函数求导,对导函数的根与区间的关系进行讨论,求出新函数的最值,求出a的范围.
(Ⅱ)求出g′(x),因为g(x)在区间(1,3)上不单调,所以g′(x)改变符号,从而得到m所满足的条件.
(Ⅲ)将图象的位置关系转化为不等式恒成立;通过构造函数,对新函数求导,对导函数的根与区间的关系进行讨论,求出新函数的最值,求出a的范围.
解答:
解:(I)∵f′(x)=
-2x+2,切点坐标(1,1),
∴切线的斜率k=f'(1)=2,
∴则切线方程为y-1=2(x-1),
即y=2x-1,
(II)∵g(x)=
x3+x2[f′(x)+2x-
+m]=
x3+(m+2)x2-2x
∴g'(x)=x2+2(m+2)x-2
∵g(x)在区间(1,3)上不是单调函数,且g'(0)=-2<0
∴
∴
故m的取值范围是(-
,-
)
(III)若在区间(1,+∞)上,函数h(x)=
f(x)+ax2-x的图象恒在直线y=2ax(x∈R)的下方等价于对任意x∈(1,+∞),不等式(a-
)x2+lnx-2ax<0恒成立
设ϕ(x)=(a-
)x2+lnx-2ax,x∈(1,+∞)
则ϕ'(x)=(2a-1)x-2a+
=(x-1)(2a-1-
)
当x∈(1,+∞)时,x-1>0,0<
<1
①若2a-1≤0,即a≤
,ϕ'(x)<0,函数ϕ(x)在区间[1,+∞)为减函数,
则当任意x∈(1,+∞)时,ϕ(x)<ϕ(1)=a-
-2a=-
-a,
只需-
-a≤0,即当-
≤a≤
时,ϕ(x)=(a-
)x2+lnx-2ax<0恒成立.
②若0<2a-1<1,即
<a<1时,令ϕ'(x)=(x-1)(2a-1-
)=0
得x=
>1,函数ϕ(x)在区间(1,
)为减函数,(
,+∞)为增函数,
则ϕ(x)∈(ϕ(
),+∞),不合题意,
③若2a-1≥1,即当a≥1时,ϕ'(x)>0,函数ϕ(x)在区间(1,+∞)为增函数
则ϕ(x)∈(ϕ(1),+∞),不合题意,
综上可知当-
≤a≤
时,ϕ(x)=(a-
)x2+lnx-2ax<0恒成立
即当-
≤a≤
时,在区间(1,+∞)上,函数h(x)=
f(x)+ax2-x的图象恒在直线y=2ax(x∈R)的下方,
综上所述.实数a的取值范围为[-
,
]
| 2 |
| x |
∴切线的斜率k=f'(1)=2,
∴则切线方程为y-1=2(x-1),
即y=2x-1,
(II)∵g(x)=
| 1 |
| 3 |
| 4 |
| x |
| 1 |
| 3 |
∴g'(x)=x2+2(m+2)x-2
∵g(x)在区间(1,3)上不是单调函数,且g'(0)=-2<0
∴
|
∴
|
故m的取值范围是(-
| 19 |
| 6 |
| 3 |
| 2 |
(III)若在区间(1,+∞)上,函数h(x)=
| 1 |
| 2 |
| 1 |
| 2 |
设ϕ(x)=(a-
| 1 |
| 2 |
则ϕ'(x)=(2a-1)x-2a+
| 1 |
| x |
| 1 |
| x |
当x∈(1,+∞)时,x-1>0,0<
| 1 |
| x |
①若2a-1≤0,即a≤
| 1 |
| 2 |
则当任意x∈(1,+∞)时,ϕ(x)<ϕ(1)=a-
| 1 |
| 2 |
| 1 |
| 2 |
只需-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
②若0<2a-1<1,即
| 1 |
| 2 |
| 1 |
| x |
得x=
| 1 |
| 2a-1 |
| 1 |
| 2a-1 |
| 1 |
| 2a-1 |
则ϕ(x)∈(ϕ(
| 1 |
| 2a-1 |
③若2a-1≥1,即当a≥1时,ϕ'(x)>0,函数ϕ(x)在区间(1,+∞)为增函数
则ϕ(x)∈(ϕ(1),+∞),不合题意,
综上可知当-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
即当-
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
综上所述.实数a的取值范围为[-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查了导数与函数单调性的关系,利用导数解决问题的能力,解决不等式恒成立及不等式有解问题一般都转化为函数的最值问题,通过导数求函数的最值,进一步求出参数的范围.

练习册系列答案
 灵星计算小达人系列答案
灵星计算小达人系列答案
相关题目
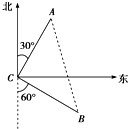 两灯塔A、B与海洋观察站C的距离都等于2
两灯塔A、B与海洋观察站C的距离都等于2| 2 |
| A、2 km |
| B、3 km |
| C、4 km |
| D、5 km |
若变量x,y满足约束条件
则Z=2x-y的最大值为( )
|
| A、2 | B、5 | C、1 | D、4 |
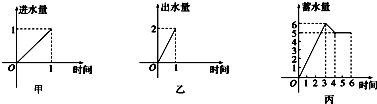
 函数y=f(x)的图象如图所示,那么,f(x)的定义域是
函数y=f(x)的图象如图所示,那么,f(x)的定义域是