题目内容
13.若函数f(x)=ax2+(a2+1)x-a(a>0)的一个零点为x0,则x0的最大值为$\sqrt{2}$-1.分析 利用求根公式求出x0,得出x0关于a的函数,令t=$\frac{a}{2}$+$\frac{1}{2a}$,则将函数转化为x0关于t的函数,利用导数求出函数的最大值即可.
解答 解:解方程得x=$\frac{-{a}^{2}-1±\sqrt{({a}^{2}+1)^{2}+4{a}^{2}}}{2a}$,
∴x0=$\frac{-{a}^{2}-1+\sqrt{{a}^{4}+6{a}^{2}+1}}{2a}$=-($\frac{a}{2}$+$\frac{1}{2a}$)+$\sqrt{\frac{{a}^{4}+6{a}^{2}+1}{4{a}^{2}}}$=-($\frac{a}{2}$+$\frac{1}{2a}$)+$\sqrt{(\frac{a}{2}+\frac{1}{2a})^{2}+1}$,
令t=$\frac{a}{2}$+$\frac{1}{2a}$,则t≥2$\sqrt{\frac{1}{4}}$=1,x0=-t+$\sqrt{{t}^{2}+1}$,
设g(t)=-t+$\sqrt{{t}^{2}+1}$,则g′(t)=-1+$\frac{t}{\sqrt{{t}^{2}+1}}$=$\frac{t-\sqrt{{t}^{2}+1}}{\sqrt{{t}^{2}+1}}$<0,
∴g(t)在[1,+∞)上单调递减,
∴g(t)≤g(1)=$\sqrt{2}$-1,
∴x0的最大值为$\sqrt{2}$-1,
故答案为:$\sqrt{2}$-1.
点评 本题考查了导数与函数单调性的关系,函数最值的计算,换元法解题思想,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.在中学生综合素质评价某个维度的测评中,分“优秀”“合格”“尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并做出频数统计表如下:
表一:男生的测评结果
表二:女生的测评结果
(1)根据题意求表一和表二中的x和y的值;并由表中统计数据写下面的2×2列联表;
(2)根据所填的列联表判断是否有95%的把握认为“测评结果是否优秀与性别有关”.
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
参考数据:
表一:男生的测评结果
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | x | 5 |
| 等级 | 优秀 | 合格 | 尚待改进 |
| 频数 | 15 | 3 | y |
| 男生 | 女生 | 合计 | |
| 优秀 | |||
| 非优秀 | |||
| 合计 |
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$(其中n=a+b+c+d)
参考数据:
| P(K2>k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8.如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,则该几何体的体积为( )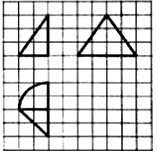

| A. | 2+π | B. | 2+4π | C. | 6+π | D. | 6+4π |
5.已知函数f(x)=6-x3,g(x)=ex-1,则这两个函数的导函数分别为( )
| A. | f′(x)=6-3x2,g′(x)=ex | B. | f′(x)=-3x2,g′(x)=ex-1 | ||
| C. | f′(x)=-3x2,g′(x)=ex | D. | f′(x)=6-3x2,g′(x)=ex-1 |