题目内容
 为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:
为了让学生了解环保知识,增强环保意识,某中学举行了一次“环保知识竞赛”,共有800名学生参加了这次竞赛.为了解本次竞赛成绩情况,从中抽取了部分学生的成绩(得分均为整数,满分为100分)进行统计.请你根据尚未完成并有局部污损的频率分布表和频率分布直方图,解答下列问题:| 分组 | 频数 | 频率 |
| 50.5~60.5 | 6 | 0.08 |
| 60.5~70.5 | 0.16 | |
| 70.5~80.5 | 15 | |
| 80.5~90.5 | 24 | 0.32 |
| 90.5~100.5 | ||
| 合计 | 75 |
(Ⅱ)补全频率分布直方图;
(Ⅲ)若对成绩在90分以上(不包含90分)的学生给予奖励,问获得奖励的学生约有多少人?
考点:频率分布直方图,频率分布表
专题:计算题,概率与统计
分析:(Ⅰ)频率分布表中频率和为1,频数=样本容量×频率;(Ⅱ)注意除以组距;(Ⅲ)总体容量×频率.
解答:
解:(Ⅰ)频数:自上到下,75×0.16=12,75-6-12-15-24=18;频率自上而下:
=0.2,
=0.24;1.
(Ⅱ)如右图,
(Ⅲ)800×0.24=192(人).
则获得奖励的学生约有192人.
| 15 |
| 75 |
| 18 |
| 75 |

(Ⅱ)如右图,
(Ⅲ)800×0.24=192(人).
则获得奖励的学生约有192人.
点评:本题考查了频率分布直方图与频率分布表的作法及作用.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
A={x|x<-1或x≥3},则∁RA等于( )
| A、{x|x<3} |
| B、{x|x<-1} |
| C、{x|-1≤x<3} |
| D、{x|x≤-3} |
已知函数f(x)=lnx+ax(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
棱长为1的正方体各顶点都在同一个球面上,则该球面的表面积等于( )
| A、2π | ||
B、
| ||
| C、3π | ||
| D、4π |
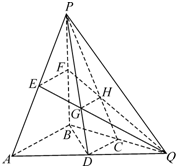 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.