题目内容
下面是水稻产量与施化肥量的一组观测数据(单位:千克/亩):
(1)将上述数据制成散点图;
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
| 施化肥量 | 15 | 20 | 25 | 30 | 35 | 40 | 45 |
| 水稻产量 | 320 | 330 | 360 | 410 | 460 | 470 | 480 |
(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗?水稻产量会一直随施化肥量的增加而增长吗?
考点:散点图
专题:作图题
分析:(1)根据所给的数据得到对应的点的坐标,在直角坐标系中,描出个点,得到散点图.
(2)从散点图中发现施化肥量与水稻产量的线性相关关系.
(2)从散点图中发现施化肥量与水稻产量的线性相关关系.
解答:
解:(1)散点图如图示:
 ,
,
(2)从图中发现数据点大致分布在一条直线附近,因此施化肥量和水稻产量近似成线性相关关系,
施化肥量由小到大时,水稻产量由小到大,但水稻产量不会一直随化肥量的增加而增长.
 ,
,(2)从图中发现数据点大致分布在一条直线附近,因此施化肥量和水稻产量近似成线性相关关系,
施化肥量由小到大时,水稻产量由小到大,但水稻产量不会一直随化肥量的增加而增长.
点评:本题考查散点图,并且由散点图得出结论,本题是一道基础题.

练习册系列答案
相关题目
已知正方体ABCD-A1B1C1D1,过顶点A1作平面α,使得直线AC和BC1与平面α所成的角都为30°,这样的平面α可以有( )
| A、4个 | B、3个 | C、2个 | D、1个 |
已知函数f(x)=lnx+ax(a∈R).
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
(1)求f(x)的单调区间;
(2)设g(x)=x2-4x+2,若对任意x1∈(0,+∞),均存在x2∈[0,1],使得f(x1)<g(x2),求a的取值范围.
已知椭圆C的上、下顶点分别为B1、B2,左、右焦点分别为F1、F2,若四边形B1F1B2F2是正方形,则此椭圆的离心率e等于( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
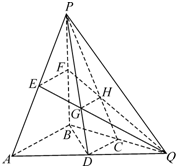 如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.
如图,在三棱锥P-ABQ中,PB⊥平面ABQ,BA=BP=BQ,D,C,E,F分别是AQ,BQ,AP,BP的中点,AQ=2BD,PD与EQ交于点G,PC与FQ交于点H,连结GH.