题目内容
6．在复平面内，若z=m2（1+i）-m（4+i）-6i，求实数m的取为何值时，复数z 是：（1）虚数
（2）对应的点在第一象限．
分析 利用代数形式的乘除运算化简．
（1）由虚部不为0求得m的取值范围；
（2）由实部和虚部均大于0列不等式组求解．
解答 解：z=m2（1+i）-m（4+i）-6i=m2+m2i-4m-mi-6i=（m2-4m）+（m2-m-6）i．
（1）z为虚数，则m2-m-6≠0，∴m≠-2且m≠3；
（2）对应的点在第一象限，则$\left\{\begin{array}{l}{{m}^{2}-4m＞0}\\{{m}^{2}-m-6＞0}\end{array}\right.$，
解得：m＜-2或m＞4．
点评 本题考查复数的代数表示法及其几何意义，是基础的计算题．
练习册系列答案
名校课堂系列答案
相关题目
16．执行如图所示的程序框图，则输出的b值等于（ ）
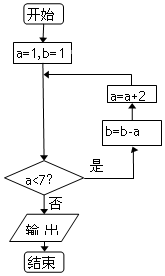
| A． | -24 | B． | -15 | C． | -8 | D． | -3 |
15．已知{an}是首项为1的等比数列，Sn是{an}的前n项和，且9S3=S6，则数列{anan+1}的前2017项和为（ ）
| A． | 22017-1 | B． | 22017-2 | C． | $\frac{1}{3}（{{4^{2017}}-1}）$ | D． | $\frac{2}{3}（{{4^{2017}}-1}）$ |
