题目内容
10.已知实数a,b满足a+b=1.(Ⅰ)求证:${a^3}+{b^3}\;≥\frac{1}{4}$;
(Ⅱ)若至少存在一个实数x,使得|x-a|+|x-b|≤5成立,求实数2a+3b的取值范围.
分析 (Ⅰ)利用立方和公式、结合配方法,即可证明;
(Ⅱ)若至少存在一个实数x,使得|x-a|+|x-b|≤5成立,则|a-b|≤5,由此求实数2a+3b的取值范围.
解答 (Ⅰ)证明:a3+b3=(a+b)(a2-ab+b2)=a2-a(1-a)+(1-a)2=$3(a-\frac{1}{2})^{2}+\frac{1}{4}$≥$\frac{1}{4}$;
(Ⅱ)解:|x-a|+|x-b|≥|x-a-x+b|=|a-b|,至少存在一个实数x,使得|x-a|+|x-b|≤5成立,则|a-b|≤5,
∵a+b=1,∴b=1-a,
∴|a-(1-a)|≤5,
∴-2≤a≤3,
∴2a+3b=3-a∈[0,5].
点评 本题考查不等式的证明,考查绝对值不等式的运用,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案 黄冈小状元同步计算天天练系列答案
黄冈小状元同步计算天天练系列答案
相关题目
18.两个粒子A,B从同一源发射出来,在某一时刻,它们的位移分别为$\overrightarrow{s_A}=({2,10}),\overrightarrow{s_B}=({4,3})$,粒子B相对粒子A的位移是$\overrightarrow s$,则$\overrightarrow s$在$\overrightarrow{s_B}$的投影是( )
| A. | $\frac{13}{5}$ | B. | $-\frac{13}{5}$ | C. | $\frac{{13\sqrt{53}}}{53}$ | D. | $-\frac{{13\sqrt{53}}}{53}$ |
2.已知i是虚数单位,复数$z=\frac{3+i}{1+i}$对应的点在第( )象限.
| A. | 一 | B. | 二 | C. | 三 | D. | 四 |
19.已知集合A={x|x2-1<0},B={x|x>0},则集合(∁RA)∪B=( )
| A. | (0,1] | B. | [1,+∞) | C. | (-∞,-1]∪[1,+∞) | D. | (-∞,-1]∪(0,+∞) |
20.若集合A={x|x≥0},且A∩B=B,则集合B可能是( )
| A. | {x|x≥2} | B. | {x|x≤1} | C. | {x|x≥-1} | D. | R |
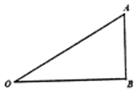 如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.
如图,某儿童公园设计一个直角三角形游乐滑梯,AO为滑道,∠OBA为直角,OB=20米,设∠AOB=θrad,一个小朋友从点A沿滑道往下滑,记小朋友下滑的时间为t秒,已知小朋友下滑的长度s与t2和sinθ的积成正比,当$θ=\frac{π}{6}$时,小朋友下滑2秒时的长度恰好为10米.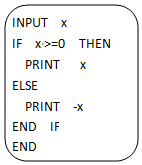 当输入的x 值为-5时,如图的程序运行的结果等于5.
当输入的x 值为-5时,如图的程序运行的结果等于5.