题目内容
1.已知数列{an}的前n项和为Sn,且4Sn+3=an2+2an.(Ⅰ)当n≥7时,a>0恒成立,求证:数列{an}从第7项起,成等差数列;
(Ⅱ)在(Ⅰ)的条件下,若数列{an}的前7项为等比数列,求数列{an}的前7项和S7.
分析 (Ⅰ)利用4Sn=an2+2an-3,再写一式,两式相减,利用当n≥7时,an>0,即可得出{an}成等差数列;
(Ⅱ)确定首项,公比,即可求{an}的前7项和S7.
解答 (Ⅰ)证明:由4Sn=an2+2an-3,4Sn+1=an+12+2an+1-3,
两式相减整理得,(an+1+an)(an+1-an-2)=0…(4分)
当n≥7时,an>0,∴an+1-an=2,
∴当n≥7时,{an}成等差数列.
(Ⅱ)解:由4S1=a12+2a1-3,得a1=3或a1=-1
又a1,a2,a3,a4,…,a7成等比数列,
∴an+1+an=0(n≤6),q=-1,
而a7>0,∴a1>0,从而a1=3.
∴S7=3-3+3-3+3-3+3=3.….(14分)
点评 本题考查等差数列的证明,考查数列的求和,考查数列递推式,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
18.某几何体的三视图如图所示,它的表面积为( )
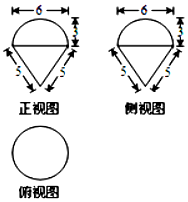

| A. | 66π | B. | 51π | C. | 48π | D. | 33π |
16.某机械研究所对新研发的某批次机械元件进行寿命追踪调查,随机抽查的200个机械元件情况如下:
若以频率为概率,现从该批次机械元件随机抽取3个,则至少有2个元件的使用寿命在30天以上的概率为( )
| 使用时间(单位:天) | 10:20 | 21:30 | 31:40 | 41:50 | 51:60 |
| 个数 | 10 | 40 | 80 | 50 | 20 |
| A. | $\frac{13}{16}$ | B. | $\frac{27}{64}$ | C. | $\frac{25}{32}$ | D. | $\frac{27}{32}$ |
 如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°
如图,在△AOC中,∠O=90°,∠C=30°,B是边OA上一点,D是边OC上一动点,且当CD=100($\sqrt{3}$-1)时,∠ADO=45°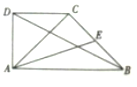 如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.
如图,在直角梯形ABCD中,已知AB∥DC,AB⊥AD,AB=2,AD=1,E为BC的中点,若$\overrightarrow{AB}•\overrightarrow{AC}=2$,则$\overrightarrow{AE}•\overrightarrow{BD}$的值为-$\frac{5}{2}$.