题目内容
已知f（x-1）=x2+4x-5，则f（x+1）= ．
考点：函数解析式的求解及常用方法
专题：函数的性质及应用
分析：将函数的表达式变形为f（x-1）=[（x-1）+3]2-9，将x+1代入表达式，整理即可．
解答：
解：∵f（x-1）=x2+4x-5=（x+2）2-9=[（x-1）+3]2-9，
∴f（x+1）=[（x+1）+3]2-9=（x+4）2-9=x2+8x+7，
故答案为：x2+8x+7．
∴f（x+1）=[（x+1）+3]2-9=（x+4）2-9=x2+8x+7，
故答案为：x2+8x+7．
点评：本题考查了求函数的表达式问题，本题属于基础题．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
直线x+y=1与直线2x+y-1=0的交点坐标是（ ）
| A、（1，0） |
| B、（0，1） |
| C、（-1，0） |
| D、（0，-1） |
若直线经过A（0，0），B（0，2）两点，则直线AB的倾斜角为（ ）
| A、30° | B、45° |
| C、90° | D、0° |
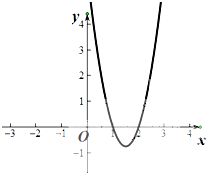已知函数f（x）=ax3+bx2+cx+1的导函数为f′（x），y=f′（x）的图象如图所示已知f（x）=
，若f（x）=2，则x的值是（ ）
|
| A、-1 | ||||
B、-1或
| ||||
C、±
| ||||
D、-1或±
|