题目内容
等差数列{an}中,已知a3=5,a2+a5=12,an=29,则n为 .
考点:等差数列的性质
专题:等差数列与等比数列
分析:设出等差数列的公差,由已知求得公差,然后代入等差数列的通项公式得答案.
解答:
解:在等差数列{an}中,设公差为d,
由a2+a5=12,得2a3+d=12,
又a3=5,
∴d=2.
由an=a3+(n-3)d=5+2(n-3)=29,
解得n=15.
故答案为:15.
由a2+a5=12,得2a3+d=12,
又a3=5,
∴d=2.
由an=a3+(n-3)d=5+2(n-3)=29,
解得n=15.
故答案为:15.
点评:本题考查了等差数列的通项公式,考查了等差数列的性质,是基础的计算题.

练习册系列答案
相关题目
已知f(x)=
,若f(x)=2,则x的值是( )
|
| A、-1 | ||||
B、-1或
| ||||
C、±
| ||||
D、-1或±
|
下列函数中与函数y=x相等的有几个?( )
(1)y=(
) 2(2)y=
(3)y=
(4)y=
.
(1)y=(
| x |
| 3 | x3 |
| x2 |
| x2 |
| x |
| A、1个 | B、2个 | C、3个 | D、4个 |
设f(x)=
,则f(f(-1))的值为( )
|
| A、0 | B、1 | C、-5 | D、5 |
已知集合M={y|x+y=2},N={(x,y)|x-y=4},那么集合M∩N为( )
| A、{x=3,y=-1} |
| B、{(x,y)|x=3或y=-1} |
| C、∅ |
| D、{(3,-1)} |
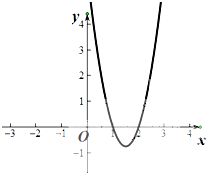 已知函数f(x)=ax3+bx2+cx+1的导函数为f′(x),y=f′(x)的图象如图所示
已知函数f(x)=ax3+bx2+cx+1的导函数为f′(x),y=f′(x)的图象如图所示