题目内容
下列集合A到集合B的对应f不是函数的有（ ）
①A={-1，0，1}，B={-1，0，1}，f：A中的数平方；
②A={0，1}，B={-1，0，1}，f：A中的数开方；
③A=Z，B=Q，f：A中的数取倒数；
④A=R，B={正实数}，f：A中的数取绝对值．
①A={-1，0，1}，B={-1，0，1}，f：A中的数平方；
②A={0，1}，B={-1，0，1}，f：A中的数开方；
③A=Z，B=Q，f：A中的数取倒数；
④A=R，B={正实数}，f：A中的数取绝对值．
| A、①②③④ | B、①③④ |
| C、①② | D、②③④ |
考点：函数的概念及其构成要素
专题：函数的性质及应用
分析：判断是否为函数，主要是看两条①A中元素全部对应出去，即都有函数值；②x对应y只能是一对一或多对一，不能出现一对多，据此判断．
解答：
解：对于①：-1和1都对应1，0对应0，故①是函数；
对于②：不能，x=1时，y=-1或1，即一个x对应两个y的值，故②不是函数；
对于③：当x=0时，
无意义，即A中元素0没有函数值，故③不是函数；
对于④：对于0∈A，其绝对值为0∉B，故④不是函数．
故选D
对于②：不能，x=1时，y=-1或1，即一个x对应两个y的值，故②不是函数；
对于③：当x=0时，
| 1 |
| 0 |
对于④：对于0∈A，其绝对值为0∉B，故④不是函数．
故选D
点评：本题重点考查了函数的对应定义，要注意正确理解、准确把握．
练习册系列答案
相关题目
已知函数f （x）在区间[a，b]上单调，且f（a）•f（b）＜0，则函数f（x）的图象与x轴在区间[a，b]内（ ）
| A、至多有一个交点 |
| B、必有唯一个交点 |
| C、至少有一个交点 |
| D、没有交点 |
直线x+y=1与直线2x+y-1=0的交点坐标是（ ）
| A、（1，0） |
| B、（0，1） |
| C、（-1，0） |
| D、（0，-1） |
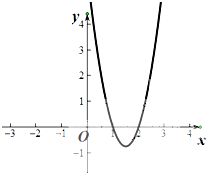已知函数f（x）=ax3+bx2+cx+1的导函数为f′（x），y=f′（x）的图象如图所示设f（x）=
，则f（f（-1））的值为（ ）
|
| A、0 | B、1 | C、-5 | D、5 |