题目内容
若曲线C1：y=x2与曲线C2：y=aex（a＞0）存在公共切线，则a的值为 ．
考点：利用导数研究曲线上某点切线方程
专题：导数的综合应用
分析：分别求出两个函数的导函数，由两函数在x处的导数相等及函数值相等求得x的值，进一步求得a的值．
解答：
解：设公切线与曲线C1切于点（x1，x12），与曲线C2切于点（x2，aex2），
则2x1=aex2=
，将aex2=2x1代入2x1=aex2=
，
可得2x2=x1+2，∴a=
．
∵a＞0，∴x2＞1，记f（x）=
，（x＞1），求得f′(x)=
，
可得f（x）在（1，2）上递增，在（2，+∞）上递减．
∴f（2）是f（x）的最大值，∴a的范围是（0，
]．
则2x1=aex2=
| aex2-x12 |
| x2-x1 |
| aex2-x12 |
| x2-x1 |
可得2x2=x1+2，∴a=
| 4(x2-1) |
| ex2 |
∵a＞0，∴x2＞1，记f（x）=
| 4(x-1) |
| ex |
| 4(2-x) |
| ex |
可得f（x）在（1，2）上递增，在（2，+∞）上递减．
∴f（2）是f（x）的最大值，∴a的范围是（0，
| 4 |
| e2 |
点评：本题考查利用导数研究曲线上某点的切线方程，过曲线上某点处的切线的斜率，就是函数在该点处的导数值，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
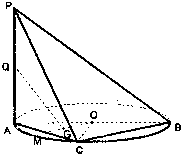如图，AB是圆O的直径，PA垂直于圆O所在的平面，C是圆0上异于A，B的点，