题目内容
已知函数f(x)=
x3-ax2+(a2-1)x+b(a,b∈R),其图象在点(1,f(1))处的切线方程为x+y-3=0.
(1)求a,b的值;
(2)求函数f(x)的极值;
(3)设g(x)=
,(x≠0),求函数g(x)在区间[1,2]上的最小值.
| 1 |
| 3 |
(1)求a,b的值;
(2)求函数f(x)的极值;
(3)设g(x)=
| 1+k•f′(x) |
| x |
考点:利用导数求闭区间上函数的最值,利用导数研究函数的单调性,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(1)由导数的运算法则可得f′(x)=x2-2ax+a2-1.由于函数f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0.可得
,解出即可;
(2)由(1)可得:f(x)=
x3-x2+
.由导数的运算法则可得f′(x)=x2-2x,分别解出f′(x)>0,f′(x)<0,即可得出单调区间;
(3)由(2)可得:g(x)=
=
=kx+
-2k,(x≠0),x∈[1,2].进而得到g′(x)=k-
=
.
对k分类讨论:当k≤0时,当k>0时,再讨论当
≥2时,当
≤1时,当1<
<2时,再利用导数与函数单调性的关系即可得出极值与最值.
|
(2)由(1)可得:f(x)=
| 1 |
| 3 |
| 8 |
| 3 |
(3)由(2)可得:g(x)=
| 1+k•f′(x) |
| x |
| 1+k(x2-2x) |
| x |
| 1 |
| x |
| 1 |
| x2 |
| kx2-1 |
| x2 |
对k分类讨论:当k≤0时,当k>0时,再讨论当
|
|
|
解答:
解:(1)f′(x)=x2-2ax+a2-1.
∵函数f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0.
∴
,即
,解得
.
∴a=1,b=
.
(2)由(1)可得:f(x)=
x3-x2+
.
f′(x)=x2-2x,
令f′(x)>0,解得x>2或x<0,∴函数f(x)在区间(-∞,0),(2,+∞)上单调递增;
令f′(x)<0,解得0<x<2,∴函数f(x)在区间(0,2)上单调递减.
∴函数f(x)在x=0时取得极大值,f(0)=
;在x=2时取得极小值,f(2)=
.
(3)g(x)=
=
=kx+
-2k,(x≠0),x∈[1,2].
g′(x)=k-
=
.
当k≤0时,g′(x)<0,函数f(x)在区间[1,2]单调递减,最小值为g(2)=2k+
-2k=
.
当k>0时,g′(x)=
.
当
≥2,即0<k≤
时,g′(x)≤0,此时函数g(x)在区间[1,2]单调递减,最小值为g(2)=2k+
-2k=
.
当
≤1时,即k≥1时,g′(x)≥0,此时函数g(x)在区间[1,2]单调递增,最小值为g(1)=k+1-2k=1-k.
当1<
<2时,即
<k<1时,当1≤x<
时,g′(x)<0,此时函数g(x)在区间[1,
)单调递减;
当
<x≤2时,g′(x)>0,此时函数g(x)在区间(
,2]单调递增.
∴函数g(x)在x=
时取得极小值,即最小值,g(
)=2
-2k.
∵函数f(x)的图象在点(1,f(1))处的切线方程为x+y-3=0.
∴
|
|
|
∴a=1,b=
| 8 |
| 3 |
(2)由(1)可得:f(x)=
| 1 |
| 3 |
| 8 |
| 3 |
f′(x)=x2-2x,
令f′(x)>0,解得x>2或x<0,∴函数f(x)在区间(-∞,0),(2,+∞)上单调递增;
令f′(x)<0,解得0<x<2,∴函数f(x)在区间(0,2)上单调递减.
∴函数f(x)在x=0时取得极大值,f(0)=
| 8 |
| 3 |
| 4 |
| 3 |
(3)g(x)=
| 1+k•f′(x) |
| x |
| 1+k(x2-2x) |
| x |
| 1 |
| x |
g′(x)=k-
| 1 |
| x2 |
| kx2-1 |
| x2 |
当k≤0时,g′(x)<0,函数f(x)在区间[1,2]单调递减,最小值为g(2)=2k+
| 1 |
| 2 |
| 1 |
| 2 |
当k>0时,g′(x)=
k(x+
| ||||||||
| x2 |
当
|
| 1 |
| 4 |
| 1 |
| 2 |
| 1 |
| 2 |
当
|
当1<
|
| 1 |
| 4 |
|
|
当
|
|
∴函数g(x)在x=
|
|
| k |
点评:本题综合考查了利用导数研究函数的单调性极值与最值、导数的几何意义、切线方程,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
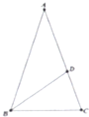 学习“三角”时,小明同学在参考书上看到求sin18°精确值的一种方法,具体如下:设等腰△ABC的顶角∠A=36°.底角∠B的平分线交腰AC于D,且BC=1(如图),则AD=BD=1,于是,在△BCD中,可得CD=2sin18°.由△BAC∽△CBD得
学习“三角”时,小明同学在参考书上看到求sin18°精确值的一种方法,具体如下:设等腰△ABC的顶角∠A=36°.底角∠B的平分线交腰AC于D,且BC=1(如图),则AD=BD=1,于是,在△BCD中,可得CD=2sin18°.由△BAC∽△CBD得| AC |
| BC |
| BD |
| CD |
| 1+2sin18° |
| 1 |
| 1 |
| 2sin18° |
| ||
| 4 |
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
| A、关于x的方程α•4x+β•2x+α=0有实数解 | ||
| B、关于x的方程α•(log4x)2+β•log4x-α=0无实数解 | ||
C、关于x的方程sinx=
| ||
D、关于x的方程cosx=
|
 已知正方体ABCD-A1B1C1D1的棱长为1.
已知正方体ABCD-A1B1C1D1的棱长为1.