题目内容
15.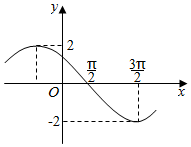 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
分析 由图象的顶点坐标求出A,由周期求出ω,通过图象经过($\frac{π}{2}$,0),求出φ,从而得到f(x)的解析式,利用诱导公式及特殊角的三角函数值即可计算求值.
解答 解:由函数的图象可得A=2,T=$\frac{2π}{ω}$=4×($\frac{3π}{2}$-$\frac{π}{2}$)=4π,解得ω=$\frac{1}{2}$.
又图象经过($\frac{π}{2}$,0),0=2sin($\frac{1}{2}$×$\frac{π}{2}$+φ),0<φ<π,
φ=$\frac{3π}{4}$,
故f(x)的解析式为f(x)=2sin($\frac{1}{2}$x+$\frac{3π}{4}$),
所以:f(2016π)=2sin($\frac{1}{2}$×2016π+$\frac{3π}{4}$)=$\sqrt{2}$.
故选:A.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求函数的解析式,考查了诱导公式及特殊角的三角函数值在三角函数化简求值中的应用,注意函数的周期的求法,考查计算能力,属于中档题.

练习册系列答案
相关题目
5.平面向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(-2,3),若$\overrightarrow{a}$∥$\overrightarrow{b}$,则实数x的值为( )
| A. | -6 | B. | $\frac{2}{3}$ | C. | -$\frac{3}{2}$ | D. | 0 |
6.在△ABC中,AB=AC,M为AC的中点,BM=$\sqrt{3}$,则△ABC面积的最大值是( )
| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
7.近年来,全国很多地区出现了非常严重的雾霾天气,而燃放烟花爆竹会加重雾霾.是否应该全面禁放烟花爆竹已成为人们议论的一个话题.一般来说,老年人(年满60周岁)从情感上不太支持禁放烟花爆竹,而中青年人(18周岁至60周岁以下)则相对理性一些.某市环保部门就是否赞成禁放烟花爆竹对400位老年人和中青年市民进行了随机问卷调查,结果如下表:
(I)有多大的把握认为“是否赞成禁放烟花爆竹”与“年龄结构”有关?请说明理由;
(Ⅱ)从上述不赞成禁放烟花爆竹的市民中按年龄结构分层抽样出13人,再从这13人中随机的挑选2人,了解它们春节期间在烟花爆竹上消费的情况.假设老年人花费500元左右,中青年人花费1000元左右.用 X表示它们在烟花爆竹上消费的总费用,求X的分布列和数学期望.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| 赞成禁放 | 不赞成禁放 | 合计 | |
| 老年人 | 60 | 140 | 200 |
| 中青年人 | 80 | 120 | 200 |
| 合计 | 140 | 260 | 400 |
(Ⅱ)从上述不赞成禁放烟花爆竹的市民中按年龄结构分层抽样出13人,再从这13人中随机的挑选2人,了解它们春节期间在烟花爆竹上消费的情况.假设老年人花费500元左右,中青年人花费1000元左右.用 X表示它们在烟花爆竹上消费的总费用,求X的分布列和数学期望.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(k2>k0) | 0.050 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
4.不等式|x-3|+|x+1|>6的解集为( )
| A. | (-∞,-2) | B. | (4,+∞) | C. | (-∞,-2)∪(4,+∞) | D. | (-2,4) |
5.在n元数集S={a1,a2,…an}中,设X(S)=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$,若S的非空子集A满足X(A)=X(S),则称A是集合S的一个“平均子集”,并记数集S的k元“平均子集”的个数为fs(k),已知集合S={1,2,3,4,5,6,7,8,9},T={-4,-3,-2,-1,0,1,2,3,4},则下列说法错误的是( )
| A. | fs(4)=fs(5) | B. | fs(4)=fT(5) | C. | fs(1)+fs(4)=fT(5)+fT(8) | D. | fs(2)+fs(3)=fT(4) |