题目内容
10．已知直线l：y=3x+3求（1）点P（4，5）关于l的对称点坐标；
（2）直线y=x-2关于l对称的直线的方程．
分析 （1）设点P（4，5）关于直线y=3x+3对称点P′的坐标为（m，n），得到关于m，n的方程组，求得m、n的值，可得P′的坐标；
（2）求出交点坐标，在直线y=x-2上任取点（2，0），得到对称点坐标，求出直线方程即可．
解答 解：（1）设点P（4，5）关于直线y=3x+3对称点P′的坐标为（m，n），
则由 $\left\{\begin{array}{l}{\frac{n-5}{m-4}•3=-1}\\{\frac{5+n}{2}=3•\frac{4+m}{2}+3}\end{array}\right.$，求得m=-2，n=7，故P′（-2，7）．
（2）由$\left\{\begin{array}{l}{y=3x+3}\\{y=x-2}\end{array}\right.$，解得：交点为$（-\frac{5}{2}，-\frac{9}{2}）$，
在直线y=x-2上任取点（2，0），
得到对称点为$（-\frac{17}{5}，\frac{9}{5}）$，
所以得到对称的直线方程为7x+y+22=0
点评 本题主要考查求一个点关于某直线的对称点的坐标的方法，利用了垂直、和中点在对称轴上这两个条件，属于中档题．
练习册系列答案
星级口算天天练系列答案
相关题目
20．已知某程序框图如图所示，则执行该程序后输出的结果是（ ）
| A． | -1 | B． | -2 | C． | 2 | D． | $\frac{1}{2}$ |
18．集合A={x|x2-2x-3＜0}，B={x||x|＜2}，则A∩B=（ ）
| A． | {x|-1＜x＜2} | B． | {x|1＜x＜3} | C． | {x|-2＜x＜1} | D． | {x|-2＜x＜2} |
15．
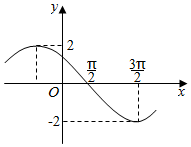已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），函数f（x）的图象如图所示，则f（2016π）的值为（ ）
已知f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜π），函数f（x）的图象如图所示，则f（2016π）的值为（ ）| A． | $\sqrt{2}$ | B． | -$\sqrt{2}$ | C． | $\sqrt{3}$ | D． | -$\sqrt{3}$ |