题目内容
6.在△ABC中,AB=AC,M为AC的中点,BM=$\sqrt{3}$,则△ABC面积的最大值是( )| A. | $\sqrt{2}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | 3 |
分析 设AB=AC=2x,三角形的顶角θ,则由余弦定理求得cosθ的表达式,进而根据同角三角函数基本关系求得sinθ,最后根据三角形面积公式表示出三角形面积的表达式,根据一元二次函数的性质求得面积的最大值.
解答  解:设AB=AC=2x,AC=x.
解:设AB=AC=2x,AC=x.
设三角形的顶角θ,则由余弦定理得cosθ=$\frac{(2x)^{2}+{x}^{2}-3}{4{x}^{2}}$=$\frac{5{x}^{2}-3}{4{x}^{2}}$
∴sinθ=$\sqrt{1-co{s}^{2}θ}$=$\sqrt{1-(\frac{5{x}^{2}-3}{4{x}^{2}})^{2}}$=$\frac{1}{4{x}^{2}}$$\sqrt{-9({x}^{2}-\frac{30}{18})^{2}+9×\frac{3{0}^{2}-1{8}^{2}}{1{8}^{2}}}$,
根据公式三角形面积S=$\frac{1}{2}$absinθ=$\frac{1}{2}$×2x×2x×$\frac{1}{4{x}^{2}}$$\sqrt{-9({x}^{2}-\frac{30}{18})^{2}+9×\frac{3{0}^{2}-1{8}^{2}}{1{8}^{2}}}$=$\frac{1}{2}$$\sqrt{-9({x}^{2}-\frac{30}{18})^{2}+9×\frac{3{0}^{2}-1{8}^{2}}{1{8}^{2}}}$,
∴当 x2=$\frac{30}{18}$时,三角形面积有最大值$\frac{1}{2}$$\sqrt{9×\frac{900-324}{324}}$=2.
故选:B.
点评 本题主要考查函数最值的应用,根据条件设出变量,根据三角形的面积公式以及三角函数的关系是解决本题的关键,利用二次函数的性质即可求出函数的最值,考查学生的运算能力.运算量较大,属于中档题.

| A. | (0,3) | B. | (0,2) | C. | (1,3) | D. | (1,+∞) |
| A. | {x|-1<x<2} | B. | {x|1<x<3} | C. | {x|-2<x<1} | D. | {x|-2<x<2} |
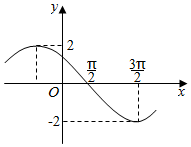 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
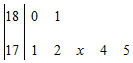 (文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.
(文科)某校女子篮球队7名运动员身高(单位:厘米)分布的茎叶图如图,已知记录的平均身高为175cm,但记录中有一名运动员身高的末位数字不清晰,如果把其末尾数记为x,那么x的值为2.