题目内容
7.近年来,全国很多地区出现了非常严重的雾霾天气,而燃放烟花爆竹会加重雾霾.是否应该全面禁放烟花爆竹已成为人们议论的一个话题.一般来说,老年人(年满60周岁)从情感上不太支持禁放烟花爆竹,而中青年人(18周岁至60周岁以下)则相对理性一些.某市环保部门就是否赞成禁放烟花爆竹对400位老年人和中青年市民进行了随机问卷调查,结果如下表:| 赞成禁放 | 不赞成禁放 | 合计 | |
| 老年人 | 60 | 140 | 200 |
| 中青年人 | 80 | 120 | 200 |
| 合计 | 140 | 260 | 400 |
(Ⅱ)从上述不赞成禁放烟花爆竹的市民中按年龄结构分层抽样出13人,再从这13人中随机的挑选2人,了解它们春节期间在烟花爆竹上消费的情况.假设老年人花费500元左右,中青年人花费1000元左右.用 X表示它们在烟花爆竹上消费的总费用,求X的分布列和数学期望.
附:${K^2}=\frac{{n{{(ad-bc)}^2}}}{(a+b)(c+d)(a+c)(b+d)}$
| P(k2>k0) | 0.050 | 0.025 | 0.010 |
| k0 | 3.841 | 5.024 | 6.635 |
分析 (Ⅰ)求出K2≈4.3956>3.841,得有95%把握认为“是否赞成禁放烟花爆竹”与“年龄结构”有关.
(Ⅱ)13人中有老年人7人,中青年人6人.那么X=2000,1500,1000.分别求出相应的概率,由此能求出X的分布列与EX.
解答 解:(Ⅰ)因为${K^2}=\frac{{400×{{(60×120-140×80)}^2}}}{140×260×200×200}=\frac{400}{91}≈4.3956>3.841$,
所以有95%把握认为“是否赞成禁放烟花爆竹”与“年龄结构”有关.…(5分)
(Ⅱ)因为140:120=7:6,所以13人中有老年人7人,中青年人6人.
那么X=2000,1500,1000.…(7分)
$P(X=2000)=\frac{C_6^2}{{C_{13}^2}}=\frac{5}{26}$,
$P(X=1500)=\frac{C_7^1C_6^1}{{C_{13}^2}}=\frac{7}{13}$,
$P(X=1000)=\frac{C_7^2}{{C_{13}^2}}=\frac{7}{26}$,
所以X的分布列为:
| X | 2000 | 1500 | 1000 |
| P | $\frac{5}{26}$ | $\frac{7}{13}$ | $\frac{7}{26}$ |
点评 本题考查离散型随机变量的分布列和数学期望的求法,是中档题,解题时要认真审题,注意排列组合知识的合理运用.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
18.集合A={x|x2-2x-3<0},B={x||x|<2},则A∩B=( )
| A. | {x|-1<x<2} | B. | {x|1<x<3} | C. | {x|-2<x<1} | D. | {x|-2<x<2} |
15.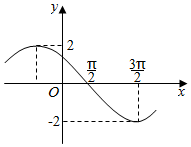 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
17.设a=2-3,b=30.5,c=log25,则a,b,c的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |