题目内容
5.在n元数集S={a1,a2,…an}中,设X(S)=$\frac{{a}_{1}+{a}_{2}+…+{a}_{n}}{n}$,若S的非空子集A满足X(A)=X(S),则称A是集合S的一个“平均子集”,并记数集S的k元“平均子集”的个数为fs(k),已知集合S={1,2,3,4,5,6,7,8,9},T={-4,-3,-2,-1,0,1,2,3,4},则下列说法错误的是( )| A. | fs(4)=fs(5) | B. | fs(4)=fT(5) | C. | fs(1)+fs(4)=fT(5)+fT(8) | D. | fs(2)+fs(3)=fT(4) |
分析 根据新定义求出k元平均子集的个数,逐一判断.
解答 解:X(S)=5,将S中的元素分成5组(1,9),(2,8),(3,7),(4,6),(5).
则fS(1)=${C}_{1}^{1}$=1,fS(2)=${C}_{4}^{1}$=4,fS(3)=${C}_{1}^{1}$•${C}_{4}^{1}$=4,fS(4)=${C}_{4}^{2}$=6,fS(5)=${{C}_{1}^{1}}_{\;}^{\;}$•${C}_{4}^{2}$=6,
同理:X(T)=0,将T中的元素分成5组(1,-1),(2,-2),(3,-3),(4,-4),(0).
则fT(1)=${C}_{1}^{1}$=1,fT(2)=${C}_{4}^{1}$=4,fT(3)=${C}_{1}^{1}$•${C}_{4}^{1}$=4,fT(4)=${C}_{4}^{2}$=6,fT(5)=${{C}_{1}^{1}}_{\;}^{\;}$•${C}_{4}^{2}$=6,fT(8)=${C}_{4}^{4}$=1,
∴fS(4)=fS(5)=6,fS(4)=fT(5)=6,fS(1)+fS(4)=fT(5)+fT(8)=7.
故选:D.
点评 本题考查了对新定义的理解,组合数公式的应用,属于中档题.

练习册系列答案
相关题目
15.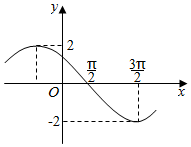 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
 已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )
已知f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π),函数f(x)的图象如图所示,则f(2016π)的值为( )| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
10.若不等式$\frac{1}{3}$<x<$\frac{1}{2}$的必要不充分条件是|x-m|<1,则实数m的取值范围是( )
| A. | [-$\frac{4}{3}$,$\frac{1}{2}$] | B. | [-$\frac{1}{2}$,$\frac{4}{3}$] | C. | (-∞,$\frac{1}{2}$) | D. | ($\frac{4}{3}$,+∞) |
17.设a=2-3,b=30.5,c=log25,则a,b,c的大小关系是( )
| A. | a<c<b | B. | a<b<c | C. | b<a<c | D. | b<c<a |