题目内容
15.已知tanα=2,则$\frac{{2{{sin}^2}α+1}}{{cos2(α-\frac{π}{4})}}$的值是( )| A. | $\frac{5}{3}$ | B. | $-\frac{13}{4}$ | C. | $\frac{13}{5}$ | D. | $\frac{13}{4}$ |
分析 利用同角三角函数基本关系式化简所求,结合已知即可计算得解.
解答 解:∵tanα=2,
∴$\frac{{2{{sin}^2}α+1}}{{cos2({α-\frac{π}{4}})}}=\frac{{2{{sin}^2}α+{{sin}^2}α+{{cos}^2}α}}{{cos({2α-\frac{π}{2}})}}=\frac{{3{{sin}^2}α+{{cos}^2}α}}{sin2α}$=$\frac{{3{{tan}^2}α+1}}{2tanα}=\frac{{3×{2^2}+1}}{2×2}=\frac{13}{4}$,
故选:D.
点评 本题主要考查了同角三角函数基本关系式在三角函数化简求值中的应用,考查了转化思想,属于基础题.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目
5.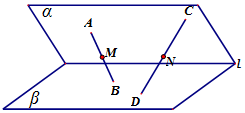 已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )
已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )
 已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )
已知平面α∩平面β=直线l,点A,C∈α,点B,D∈β,且A,B,C,D∉l,点M,N分别是线段AB,CD的中点.( )| A. | 当|CD|=2|AB|时,M,N不可能重合 | |
| B. | M,N可能重合,但此时直线AC与l不可能相交 | |
| C. | 当直线AB,CD相交,且AC∥l时,BD可与l相交 | |
| D. | 当直线AB,CD异面时,MN可能与l平行 |
6.已知变量x,y满足约束条件$\left\{\begin{array}{l}x+2y≤3\\ x+3y≥-k\\ y≤1\end{array}\right.$(k∈Z),且z=2x+y的最大值为6,则k的值为( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
3.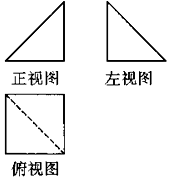 如图,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的最大面的面积是( )
如图,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的最大面的面积是( )
 如图,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的最大面的面积是( )
如图,一个多面体的正视图和侧视图是两个全等的等腰直角三角形且直角边长为2,俯视图是边长为2的正方形,则该多面体的最大面的面积是( )| A. | 2 | B. | $4\sqrt{2}$ | C. | $2\sqrt{2}$ | D. | $2\sqrt{3}$ |
10.已知命题p:x2+x-2>0,命题q:{x|f(x)=lg(2x-3)},则p是q的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
7.如果θ是第三象限的角,那么( )
| A. | sinθ>0 | B. | cosθ>0 | C. | tanθ>0 | D. | 以上都不对 |
1.已知f(x)=x2-2x+3,则g(x)=f(2-x2)的单调增区间是( )
| A. | [-1,0]及[1,+∞) | B. | [-$\sqrt{3}$,0]及[$\sqrt{3}$,+∞) | C. | (-∞,-1]及[0,1] | D. | (-∞,-$\sqrt{3}$]及[0,$\sqrt{3}$] |