题目内容
6.己知椭圆$\frac{x^2}{25}+\frac{y^2}{m^2}$=1 (m>0)的右焦点为F1(4,0),则m=( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
分析 求出椭圆的a,b,c,解方程$\sqrt{25-{m}^{2}}$=4,即可得到m的值.
解答 解:椭圆$\frac{x^2}{25}+\frac{y^2}{m^2}$=1的a=5,b=m,
c=$\sqrt{25-{m}^{2}}$,
由题意可得$\sqrt{25-{m}^{2}}$=4,
解得m=3.
故选:C.
点评 本题考查椭圆的焦点的运用,考查椭圆的方程和运用,注意椭圆的a,b,c的关系,考查运算能力,属于基础题.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
16.若椭圆x2+my2=1的焦距为2,则m的值是( )
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
14.执行如图所示的程序框图,如果输出的k的值为3,则输入的a的值可以是( )
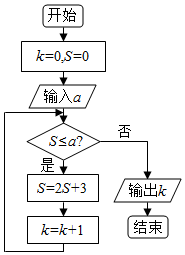

| A. | 20 | B. | 21 | C. | 22 | D. | 23 |
1.直线3x-4y-4=0被圆x2+y2-6x=0截得的弦长为( )
| A. | $2\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 2 |
11.已知双曲线C的渐近线方程为3x±2y=0,且经过点$(4,3\sqrt{2})$,则该双曲线的方程为( )
| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
18.已知$\overrightarrow x•\overrightarrow y=0$,且$|\overrightarrow x|=|\overrightarrow y|=2$,若$\overrightarrow m=λ\overrightarrow x+(1-λ)\overrightarrow y$(0≤λ≤1),则$|\overrightarrow m|$的取值范围是( )
| A. | [1,2] | B. | $[\sqrt{2},2]$ | C. | [0,2] | D. | [2,4] |
15.多项式(x2-x+2)5展开式中x3的系数为( )
| A. | -200 | B. | -160 | C. | -120 | D. | -40 |
 在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.
在三棱柱PBC-QAD中,侧面ABCD为矩形,PA⊥CD.