题目内容
1.直线3x-4y-4=0被圆x2+y2-6x=0截得的弦长为( )| A. | $2\sqrt{2}$ | B. | 4 | C. | $4\sqrt{2}$ | D. | 2 |
分析 先将圆化为标准方程,然后利用点到直线的距离求弦长.
解答 解:圆的标准方程为(x-3)2+y2=9,圆心为P(3,0),半径为r=3.
∴圆心到直线3x-4y-4=0的距离d=$\frac{|3×3-4|}{\sqrt{{3}^{2}+(-4)^{2}}}=1$.
∴弦长l=2$\sqrt{{r}^{2}-{d}^{2}}=2\sqrt{9-1}=4\sqrt{2}$,
故选:C.
点评 本题主要考查了直线与圆的位置关系以及弦长公式,将圆化为标准方程是解决本题的关键,是基础题.

练习册系列答案
相关题目
16.已知圆x2+y2-2x-4y+a=0上有且仅有一个点到直线3x-4y-15=0的距离为1,则实数a的取值情况为( )
| A. | (-∞,5) | B. | -4 | C. | -4或20 | D. | -11 |
13. 设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
 设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )
设全集U={1,2,3,4,5,6},集合A={1,2,4},B={1,3,5},则下列Venn图中阴影部分表示的集合是( )| A. | {1} | B. | {2,4} | C. | {3,5} | D. | {2,3,4,5} |
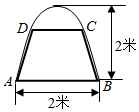 如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.
如图,有一块抛物线形钢板,其下口宽为2米,高为2米.计划将此钢板切割成等腰梯形的形状,下底AB是抛物线的下口,上底CD的端点在抛物线上.