题目内容
11.已知双曲线C的渐近线方程为3x±2y=0,且经过点$(4,3\sqrt{2})$,则该双曲线的方程为( )| A. | $\frac{x^2}{8}-\frac{y^2}{9}=1$ | B. | $\frac{y^2}{9}-\frac{x^2}{16}=1$ | C. | $\frac{x^2}{8}-\frac{y^2}{18}=1$ | D. | $\frac{y^2}{18}-\frac{x^2}{16}=1$ |
分析 设出以3x±2y=0为渐近线的双曲线方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}=λ(λ≠0)$,代入点的坐标求得λ,则答案可求.
解答 解:∵双曲线C的渐近线方程为3x±2y=0,
∴设双曲线方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}=λ(λ≠0)$,
又双曲线过点$(4,3\sqrt{2})$,
∴$\frac{{4}^{2}}{4}-\frac{(3\sqrt{2})^{2}}{9}=λ$,解得:λ=2,
∴双曲线方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{9}=2$,即$\frac{{x}^{2}}{8}-\frac{{y}^{2}}{18}=1$.
故选:C.
点评 本题考查双曲线的标准方程,以$y=±\frac{b}{a}x$为渐近线的双曲线方程可设为$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}=λ(λ≠0)$,是中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
2.要计算$1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{2016}$的结果,下面的程序框图中的横线上可以填( )


| A. | n<2016? | B. | n≤2016? | C. | n>2016? | D. | n≥2016? |
19.下列说法错误的是( )
| A. | 命题“若x2-3x+2=0,则x=1”的逆否命题为:“若x≠1,则x2-3x+2≠0” | |
| B. | 对于命题p:?x0∈R,x${\;}_{0}^{2}$+x0+1<0,则¬p:?x∈R,x2+x+1≥0 | |
| C. | 若m,n∈R,“lnm<lnn”是“em<en”的充分不必要条件 | |
| D. | 若p∧q为假命题,则p、q均为假命题 |
16.函数f(x)的部分图象如图所示,则f(x)的解析式可以是( )
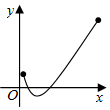

| A. | f(x)=2x+lgx+2 | B. | f(x)=2x+lgx-2 | C. | f(x)=2x-lgx+2 | D. | f(x)=2x-lgx-2 |
1.已知i为虚数单位,a∈R,若(a2+2a-3)+(a+3)i为纯虚数,则a的值为( )
| A. | 1 | B. | -3 | C. | -3或1 | D. | 3或1 |