题目内容
7.二项式${(3{x^2}-\frac{2}{{\root{3}{x}}})^7}$展开式中含有常数项,则常数项是第( )项.| A. | 6 | B. | 5 | C. | 8 | D. | 7 |
分析 根据展开式中含有常数项,可得x的幂指数等于零有解,求得r的值,可得常数项是第(r+1)项.
解答 解:二项式${(3{x^2}-\frac{2}{{\root{3}{x}}})^7}$展开式的通项公式为Tr+1=${C}_{7}^{r}$•37-r•(-2)r•${x}^{14-\frac{7r}{3}}$,根据展开式中含有常数项,
可得14-$\frac{7r}{3}$=0有解,故r=6,故常数项是第7项,
故选:D.
点评 本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
15.函数f(x)=x3-12x的极小值点是( )
| A. | 2 | B. | -2 | C. | -16 | D. | 16 |
2.已知数列{an}的通项公式为an=3n-50,则当n等于( )时,Sn取得最小值?
| A. | 16 | B. | 17 | C. | 18 | D. | 16或17 |
16.已知A(4,0),B(2,2)为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1内的点,M是椭圆上的动点,则|MA|+|MB|的最小值是( )
| A. | 10+2$\sqrt{10}$ | B. | 10+$\sqrt{10}$ | C. | 10-2$\sqrt{10}$ | D. | 10-$\sqrt{10}$ |
17.sin315°的值为( )
| A. | -$\frac{\sqrt{3}}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
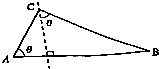 某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.
某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后,再沿南偏东θ方向走4min到达B点,AB=100m,求他走路的最小速度.