题目内容
16.已知A(4,0),B(2,2)为椭圆$\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{9}$=1内的点,M是椭圆上的动点,则|MA|+|MB|的最小值是( )| A. | 10+2$\sqrt{10}$ | B. | 10+$\sqrt{10}$ | C. | 10-2$\sqrt{10}$ | D. | 10-$\sqrt{10}$ |
分析 由椭圆的定义可知,MA+MB=10+|MB|-|MF|.当M在直线BF与椭圆交点上时,在第一象限交点时有|MB|-|MF|=-|BF|,在第三象限交点时有|MB|-|MF|=|BF|.显然当M在直线BF与椭圆第一象限交点时,|MA|+|MB|有最小值.
解答 解:A为椭圆右焦点,左焦点F(-4,0),B在椭圆内,
∴|MA|+|MF|=2a=10,
于是|MA|+|MB|=10+|MB|-|MF|.
当M不在直线BF与椭圆交点上时,M、F、B三点构成三角形,
于是|MB|-|MF|<|BF|,
而当M在直线BF与椭圆交点上时,
在第一象限交点时,有|MB|-|MF|=-|BF|,
在第三象限交点时有|MB|-|MF|=|BF|.
显然当M在直线BF与椭圆第一象限交点时,|MA|+|MB|有最小值,
∴最小值|MA|+|MB|=10+|MB|-|MF|=10-|BF|=10-$\sqrt{(2+4)^{2}+(2-0)^{2}}$=10-2$\sqrt{10}$,
故答案为:10-2$\sqrt{10}$.
点评 本题考查椭圆的定义及最值的求法,注意转化思想,以及三点共线求最值的方法,解题时要熟练掌握定义法的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
6.已知函数f(x)=ex(x2+2ax+b)在x=-1处取得极大值t,则t的取值范围是( )
| A. | ($\frac{2}{e}$,+∞) | B. | (-∞,$\frac{2}{e}$) | C. | (-$\frac{2}{e}$,+∞) | D. | (-∞,-$\frac{2}{e}$) |
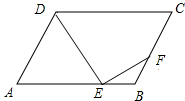 如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.
如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.