题目内容
19.函数y=-$\frac{1}{3}$cos(2x-$\frac{π}{4}}$)的单调增区间是[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.分析 利用余弦函数的单调性,求得函数y=-$\frac{1}{3}$cos(2x-$\frac{π}{4}}$)的单调增区间.
解答 解:y=-$\frac{1}{3}$cos(2x-$\frac{π}{4}}$)的单调增区间,即函数y=$\frac{1}{3}$cos(2x-$\frac{π}{4}}$)的减区间,
令2kπ≤2x-$\frac{π}{4}$≤2kπ+π,求得kπ+$\frac{π}{8}$≤x≤kπ+$\frac{5π}{8}$,
故函数的增区间为[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z,
故答案为:[kπ+$\frac{π}{8}$,kπ+$\frac{5π}{8}$],k∈Z.
点评 本题主要考查余弦函数的单调性,属于基础题.

练习册系列答案
 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案
相关题目
14.已知等差数列{an}中,且a4+a12=10,则前15项和S15=( )
| A. | 15 | B. | 20 | C. | 21 | D. | 75 |
9.已知等差数列{an}的前n项和记为Sn,若a4+a6+a8=15,则S11的值为( )
| A. | 55 | B. | $\frac{55}{2}$ | C. | 165 | D. | $\frac{165}{2}$ |
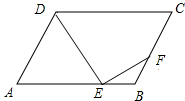 如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.
如图,在平行四边形ABCD中,AB=4,AD=2,∠BAD=60°,E,F分别为AB,BC上的点,且AE=2EB,CF=2FB.