题目内容
3．
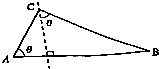某人以速度vm/min的速度从点A沿东偏北θ方向走3min到达点C后，再沿南偏东θ方向走4min到达B点，AB=100m，求他走路的最小速度．
分析 AC=3v，BC=4v，∠ACB=|90°-2θ|，由余弦定理，求出v2=$\frac{10{0}^{2}}{25-24sin2θ}$，即可求他走路的最小速度．
解答 解：AC=3v，BC=4v，∠ACB=|90°-2θ|，
由余弦定理可得AB2=AC2+BC2-2AC•BC•cos∠ACB，
所以1002=9v2+16v2-2•3v•4v•sin（2θ）
所以1002=25v2-24v2sin（2θ）
所以 v2=$\frac{10{0}^{2}}{25-24sin2θ}$，
因为sin2θ的最小值为-1，
所以25-24sin2θ的最大值为49，
所以v2的最小值为$\frac{10{0}^{2}}{49}$，
所以v的最小值为$\frac{100}{7}$m/min
点评 本题考查利用数学知识解决实际问题，考查余弦定理的运用，考查三角函数知识，属于中档题．
练习册系列答案
相关题目
13．下列函数中，最小正周期为$\frac{π}{2}$的是（ ）
| A． | y=sin$\frac{x}{2}$ | B． | y=2sinx | C． | y=sin4π | D． | y=sin（-4x） |
11．某中学在高三年级开设大学先修课程（线性代数），共有50名同学选修，其中男同学30名，女同学20名．为了对这门课程的数学效果进行评估，学校按性别分别采用分成抽样的方法抽取5人进行考核．
（1）求抽取的5人中男、女同学的人数；
（2）考核的第一轮是答辩，顺序由已抽取的甲、乙等5位同学按抽签方式决定．设甲、乙两位同学间隔的人数为X，X的分布列为
求数学期望EX；
（3）考核的第二轮是笔试：5位同学的笔试成绩分别为115，122，105，111，109；结合第一轮的答辩情况，他们的考核成绩分别为125，132，115，121，119．这5位同学笔试成绩与考核成绩的方差分别记为s12，s22，试比较s12与s22的大小．（只需写出结论）
（1）求抽取的5人中男、女同学的人数；
（2）考核的第一轮是答辩，顺序由已抽取的甲、乙等5位同学按抽签方式决定．设甲、乙两位同学间隔的人数为X，X的分布列为
| X | 3 | 2 | 1 | 0 |
| P | $\frac{1}{10}$ | b | $\frac{3}{10}$ | a |
（3）考核的第二轮是笔试：5位同学的笔试成绩分别为115，122，105，111，109；结合第一轮的答辩情况，他们的考核成绩分别为125，132，115，121，119．这5位同学笔试成绩与考核成绩的方差分别记为s12，s22，试比较s12与s22的大小．（只需写出结论）
6．已知函数f（x）=ex（x2+2ax+b）在x=-1处取得极大值t，则t的取值范围是（ ）
| A． | （$\frac{2}{e}$，+∞） | B． | （-∞，$\frac{2}{e}$） | C． | （-$\frac{2}{e}$，+∞） | D． | （-∞，-$\frac{2}{e}$） |