题目内容
8.在等比数列{an}中,已知a1=3,公比q≠1,等差数列{bn}满足b1=a1,b4=a2,b13=a3.(1)求数列{an}与{bn}的通项公式;
(2)记cn=an+bn,求数列{cn}的前n项和Sn.
分析 (1)设等比数列{an}的公比为q≠1,等差数列{bn}的公差为d,运用等差数列和等比数列的通项公式,列方程组,可得公比和公差,进而得到所求通项公式;
(2)求得cn=an+bn=3n+(2n+1),运用数列的求和方法:分组求和,结合等比数列和等差数列的求和公式,计算即可得到所求和.
解答 解:(1)设等比数列{an}的公比为q≠1,等差数列{bn}的公差为d.
由b1=a1,b4=a2,b13=a3,
得$\left\{\begin{array}{l}3q=3+3d\\ 3{q^2}=3+12d\end{array}\right.$⇒$\left\{\begin{array}{l}q=1+d\\{q^2}=1+4d\end{array}\right.$⇒q=3或1(舍去),d=2,
所以an=3n,bn=2n+1.
(2)由题意,得cn=an+bn=3n+(2n+1),
Sn=c1+c2+…+cn=(3+5+7+…+2n+1)+(3+32+…+3n)
=$\frac{n(3+2n+1)}{2}$+$\frac{{3(1-{3^n})}}{1-3}$=$\frac{{{3^{n+1}}}}{2}$+n2+2n-$\frac{3}{2}$.
点评 本题考查等差数列和等比数列的通项公式和求和公式的运用,考查数列的求和方法:分组求和,考查化简整理的运算能力,属于中档题.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案
相关题目
3.若cosα=$\frac{1}{2}$,α∈(0,π),则cos($\frac{π}{2}$-α)=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{\sqrt{3}}{2}$ |
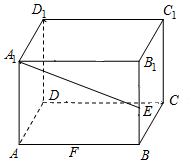 已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.
已知在长方体ABCD-A1B1C1D1中,AD=AA1=1,AB=2,点F是AB边上动点,点E是棱B1B的中点.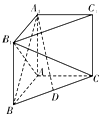 如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1,D为BC的中点.
如图,在三棱柱ABC-A1B1C1中,A1A⊥平面ABC,AB⊥AC,AB=AC=AA1,D为BC的中点.