题目内容
10. 如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间,即${a^2}<\int_a^{a+1}{{x^2}dx<{{(a+1)}^2}}$.类比之,若对?n∈N+,不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}<1n4<\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立,则实数k等于2.
如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间,即${a^2}<\int_a^{a+1}{{x^2}dx<{{(a+1)}^2}}$.类比之,若对?n∈N+,不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}<1n4<\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立,则实数k等于2.
分析 利用定义可得即$\frac{k}{n}<k[ln(n+1)-lnn]<\frac{k}{n+1}$相加求出即可.
解答 解:因为$\frac{k}{n}<\int{\begin{array}{l}{n+1}\\ n\end{array}}\frac{k}{x}dx<\frac{k}{n+1}$,
所以$\frac{k}{n}$<klnx|${\;}_{n}^{n+1}$<$\frac{k}{k+1}$,
即$\frac{k}{n}<k[ln(n+1)-lnn]<\frac{k}{n+1}$,
同理$\frac{k}{n+1}<k[ln(n+2)-ln(n+1)]<\frac{k}{n+2}$,…,$\frac{k}{2n-1}<k[ln(2n)-ln(2n-1)]<\frac{k}{2n}$,
累加得$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}<k[ln(2n)-lnn)]$$<\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$
所以ln4=k[ln(2n)-lnn)],
所以ln4=kln2,
故k=2,
故答案为:2.
点评 本题考查定积分的简单应用,根据定积分的定义得到即$\frac{k}{n}<k[ln(n+1)-lnn]<\frac{k}{n+1}$是解题的关键,本题是一道中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
20.在我国古代著名的数学专著《九章算术》里有一段叙述:今有良马与驽马发长安至齐,齐去长安一千一百二十五里,良马初日行一百零三里,日增一十三里;驽马初日行九十七里,日减半里;良马先至齐,复还迎驽马,二马相逢.问:几日相逢?( )
| A. | 8日 | B. | 9日 | C. | 12日 | D. | 16日 |
1.由于空气污染严重,某工厂生产了两种供人们外出时便于携带的呼吸装置,其质量按测试指标划分:指标大于或等于82为合格品,小于82为次品.现随机抽取这两种装置各100件进行检测,检测结果统计如下:
(Ⅰ)试分别估计装置甲、装置乙为合格品的概率;
(Ⅱ)生产一件装置甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件装置乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的条件下,
(1)记X为生产一件装置甲和生产一件装置乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件装置乙所获得的利润不少于140元的概率.
| 测试指标 | [70,76] | [76,82] | [82,88] | [88,94] | [94,100] |
| 装置甲 | 8 | 12 | 40 | 32 | 8 |
| 装置乙 | 7 | 18 | 40 | 29 | 6 |
(Ⅱ)生产一件装置甲,若是合格品可盈利40元,若是次品则亏损5元;生产一件装置乙,若是合格品可盈利50元,若是次品则亏损10元.在(Ⅰ)的条件下,
(1)记X为生产一件装置甲和生产一件装置乙所得的总利润,求随机变量X的分布列和数学期望;
(2)求生产5件装置乙所获得的利润不少于140元的概率.
18.已知集合A={x|x2-2x≤0},B={-1,0,1,2},则A∩B=( )
| A. | [0,2] | B. | {0,1,2} | C. | (-1,2) | D. | {-1,0,1} |
2.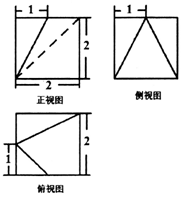 如图为一个多面体的三视图,则该多面体的体积为( )
如图为一个多面体的三视图,则该多面体的体积为( )
 如图为一个多面体的三视图,则该多面体的体积为( )
如图为一个多面体的三视图,则该多面体的体积为( )| A. | $\frac{20}{3}$ | B. | 7 | C. | $\frac{22}{3}$ | D. | $\frac{23}{3}$ |
20.在等差数列{an}中,若a6+a8+a10=72,则2a10-a12的值为( )
| A. | 20 | B. | 22 | C. | 24 | D. | 28 |
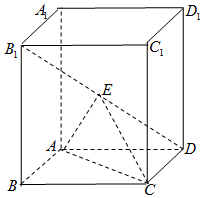 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.