题目内容
19.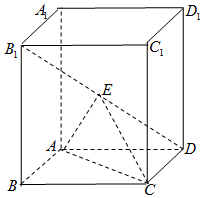 如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.
如图,四棱柱ABCD-A1B1C1D1中,底面ABCD为菱形,AA1⊥底面ABCD,E为B1D的中点.(Ⅰ)证明:平面ACE⊥平面ABCD;
(Ⅱ)若二面角D-AE-C为60°,AA1=AB=1,求三棱锥C-AED的体积.
分析 (Ⅰ)连接BD,设AC与BD的交点为F,连接EF,则EF∥BB1,从而EF⊥平面ABCD,由此能证明平面ACE⊥平面ABCD.
(Ⅱ)以F为坐标原点,以FC,FD,FE为x,y,z轴,建立空间直角坐标系,利用向量法能求出三棱锥C-ADE的体积.
解答 证明:(Ⅰ)连接BD,设AC与BD的交点为F,连接EF,
因为E为B1D中点,F为BD中点,
所以EF∥BB1,
因为BB1⊥平面ABCD,
所以EF⊥平面ABCD,
又因为EF在平面ACE内,
所以平面ACE⊥平面ABCD.(6分)
解:(Ⅱ)由于四边形ABCD是菱形,所以以F为坐标原点,
分别以FC,FD,FE为x,y,z轴,建立空间直角坐标系,
设FA=a,FD=b,有a2+b2=1,
A(-a,0,0),C(a,0,0),D(0,b,0),$E(0,0,\frac{1}{2})$,
$\overrightarrow{AE}=(a,0,\frac{1}{2})$,$\overrightarrow{AD}=(a,b,0)$,
设平面ADE的法向量为$\overrightarrow{n_1}=(b,-a,-2ab)$,
平面ACE的法向量为$\overrightarrow{n_2}=(0,1,0)$,(8分)
由题意知$cos{60°}=|cos<\overrightarrow{n_1},\overrightarrow{n_2}>|=\frac{{|\overrightarrow{n_1}•\overrightarrow{n_2}|}}{{|\overrightarrow{n_1}|•|\overrightarrow{n_2}|}}=\frac{1}{2}$,解得$a=b=\frac{{\sqrt{2}}}{2}$.(10分)
所以菱形ABCD为正方形,
所以三棱锥C-ADE的体积$V=\frac{1}{3}×EF×\frac{1}{2}×AD×CD=\frac{1}{12}$.(12分)
点评 本题以四棱柱为载体,考查平面与平面垂直,以及二面角、体积等问题,考查空间中线线、线面、面面间的位置关系等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、数形结合思想、函数与方程思想,是中档题.

| 顾 客 产 品 | a1 | a2 | a3 | a4 | a5 | a6 | a7 | a8 | a9 | a10 | a11 | a12 | a13 | a14 | a15 |
| A | 1 | 1 | 1 | 1 | 1 | ||||||||||
| B | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | |||||||
| C | 1 | 1 | 1 | 1 | 1 | 1 | 1 | ||||||||
| D | 1 | 1 | 1 | 1 | 1 | 1 |
(Ⅱ)为推广新产品,超市向购买两种以上(含两种)新产品的顾客赠送2元电子红包.现有甲、乙、丙三人在该超市购物,记他们获得的电子红包的总金额为X,求随机变量X的分布列和数学期望;
(Ⅲ)若某顾客已选中产品B,为提高超市销售业绩,应该向其推荐哪种新产品?(结果不需要证明)
 如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间,即${a^2}<\int_a^{a+1}{{x^2}dx<{{(a+1)}^2}}$.类比之,若对?n∈N+,不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}<1n4<\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立,则实数k等于2.
如图所示,由直线x=a,x=a+1(a>0),y=x2及x轴围成的曲边梯形的面积介于小矩形与大矩形的面积之间,即${a^2}<\int_a^{a+1}{{x^2}dx<{{(a+1)}^2}}$.类比之,若对?n∈N+,不等式$\frac{k}{n+1}+\frac{k}{n+2}+…+\frac{k}{2n}<1n4<\frac{k}{n}+\frac{k}{n+1}+…+\frac{k}{2n-1}$恒成立,则实数k等于2.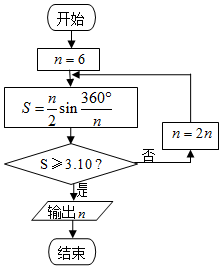 公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )
公元263年左右,我国古代数学家刘徽用圆内接正多边形的面积去逼近圆的面积求圆周率π,刘徽称这个方法为“割圆术”,并且把“割圆术”的特点概括为“割之弥细,所失弥少,割之又割,以至于不可割,则与圆周合体而无所失矣”下图是根据刘徽的“割圆术”思想设计的一个程序框图.若运行该程序,则输出的n的值为:(参考数据:$\sqrt{3}$≈1.732,sin15°≈0.2588,sin7.5°≈0.1305)( )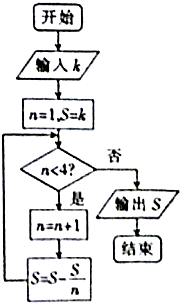 我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )
我国古代数学著作《九章算术》有如下问题:“今有器中米,不知其数,前人取半,中人三分取一,后人四分取一,余米一斗五升.问,米几何?”如图是解决该问题的程序框图,执行该程序框图,若输出的S=1.5(单位:升),则输入k的值为( )