题目内容
4.已知曲线C上的任意一点到点F(1,0)的距离与到直线x=-1的距离相等,直线l过点A(1,1),且与C交于P,Q两点;(Ⅰ)求曲线C的方程;
(Ⅱ)若A为PQ的中点,求三角形OPQ的面积.
分析 (Ⅰ)利用曲线C上任意一点到点F(1,0)的距离与到直线x=-1的距离相等,可知曲线C的轨迹是以F(1,0)为焦点的抛物线,从而可求曲线C的方程;
(Ⅱ)求出直线l的方程,与抛物线方程联立,利用韦达定理,即可求三角形OPQ的面积.
解答 解:(Ⅰ)∵曲线C上任意一点到点F(1,0)的距离与到直线x=-1的距离相等.
∴曲线C的轨迹是以F(1,0)为焦点的抛物线
∴曲线C的方程为y2=4x.…(4分)
(Ⅱ)设P(x1,y1),Q(x2,y2),则y1+y2=2
因为y12=4x1,y22=4x2,
所以作差,可得直线l斜率为2,…(6分)
所以直线方程为y-1=2(x-1),即y=2x-1.
此时直线l与抛物线相交于两点.…(7分)
设T为l与x的交点,则|OT|=$\frac{1}{2}$,…(8分)
由y=2x-1与y2=4x,消去x得y2-2y-2=0,…(9分)
所以y1+y2=2,y1y2=-2,…(10分)
所以三角形OPQ的面积为S=$\frac{1}{2}$|OT||y1-y2|=$\frac{\sqrt{3}}{2}$.…(12分)
点评 本题考查轨迹方程的求法,考查直线与抛物线的位置关系,解题的关键是正确运用抛物线的定义,正确运用韦达定理.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
14.已知直线x+(m2-m)y=4m-1与直线2x-y-5=0垂直,则m的值为( )
| A. | -1 | B. | 2 | C. | -1或2 | D. | 1 |
15.函数f(x)=ax+$\frac{1}{a}$(2-x),其中a>0,记f(x)在区间[0,2]上的最小值为g(a),则函数g(a)的最大值为( )
| A. | $\frac{1}{2}$ | B. | 0 | C. | 1 | D. | 2 |
9.“x2-4x<0”的一个充分不必要条件为( )
| A. | 0<x<4 | B. | 0<x<2 | C. | x>0 | D. | x<4 |
13.已知椭圆的焦点F1(0,-1),F2(0,1),P为椭圆上一动点,且|F1F2|是|PF1|与|PF2|的等差中项,则椭圆的标准方程为( )
| A. | $\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1 | B. | $\frac{{x}^{2}}{3}$+$\frac{{y}^{2}}{4}$=1 | C. | x2+$\frac{{y}^{2}}{3}$=1 | D. | $\frac{{x}^{2}}{3}$+y2=1 |
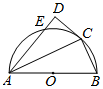 已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.
已知AB为半圆O的直径,C为半圆上一点,CD是半圆的切线,AC平分∠BAD,AD交半圆于点E.